-
9. БУДЬ ЛАСКА Розв'яжіть рівняння 2sin^2 (2pi - x) - cos(2x + pi/2) + 6cos^2 (x - pi) = 3
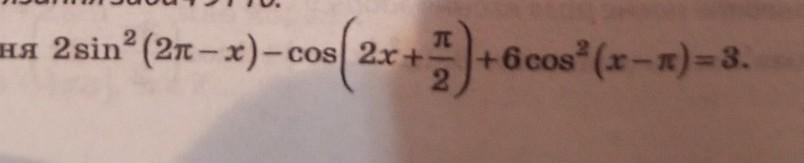
Ответы 1
-
1.[ 2 - 2\cos^2(x) - \sin(2x) + 6\cos^2(x) = 3]
2.[ 4\cos^2(x) - \sin(2x) = 1]
[ 4\cos^2(x) - 2\sin(x)\cos(x) = 1 ]
[ 4\cos^2(x) - 2\sin(x)\cos(x) - 1 = 0 ]
[ (2\cos(x) - 1)^2 = 0 ]
Отсюда получаем:
[ 2\cos(x) - 1 = 0 ]
[ 2\cos(x) = 1 ]
[ \cos(x) = \frac{1}{2} ]
у нас два решения:
[ x = \frac{\pi}{3} + 2\pi k ]
[ x = \frac{5\pi}{3} + 2\pi k ]
где ( k ) - целое число.
Объяснение:
можно лучший ответ?
-
Автор:
ninaztmx - 2 года назад
-
1
-
-
Добавить свой ответ
Еще вопросы
-
Хронологічна таблиця Тараса Бульби
-
Предмет:
Литература -
Автор:
godiva - 2 года назад
-
Ответов:
1 -
Смотреть
-
- В основі прямої призми лежить рівнобедрений трикутник з основою 12 см і бічною стороною 10 см. Обчислити об’єм цієї призми, якщо діагональ меншої бічної грані дорівнює 26 см.
-
Придумайте и запишите пары предложений так, чтобы в первом
было вопросительное
-
Предмет:
Русский язык -
Автор:
jamaridoyle - 2 года назад
-
Ответов:
2 -
Смотреть
-
- Вершина правильної чотирикутної піраміди рівновіддалена від сторін основи на 26 см, а від площини основи на 24 см. Знайдіть площу основи піраміди.
How much to ban the user?
1 hour
1 day
100 years
