-
Помогите пожалуйста (скрин) и написать на листке бумаги желательно :)
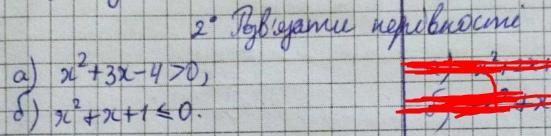
-
Предмет:
Алгебра -
Автор:
sarahwhite - 2 года назад
-
Ответы 1
-
Ответ:
a) Для розв'язання нерівності \( x^2 + 3x - 4 > 0 \) можемо скористатися методом дослідження знаків.
1. Знаходимо корені квадратного рівняння \( x^2 + 3x - 4 = 0 \):
\[ x^2 + 3x - 4 = (x - 1)(x + 4) = 0 \]
Отримуємо корені \( x = 1 \) і \( x = -4 \).
2. Проводимо дослідження знаків на проміжках, утворених коренями:
- \( (-\infty, -4) \): Вибираємо \( x = -5 \) (відсутній множник зі змінними) - від'ємний результат.
- \( (-4, 1) \): Вибираємо \( x = 0 \) - додатний результат.
- \( (1, +\infty) \): Вибираємо \( x = 2 \) - додатний результат.
Таким чином, розв'язком нерівності \( x^2 + 3x - 4 > 0 \) є \( x \in (-4, 1) \).
(5) Для розв'язання нерівності \( x^2 + x + 1 \leq 0 \), згадаймо, що квадратне вираження \( x^2 + x + 1 \) завжди буде не менше за 0 для будь-якого дійсного \( x \), оскільки це сума квадратів, яка завжди не менше за 0. Тому ця нерівність не має розв'язків в області дійсних чисел.
-
Автор:
jettwfnj - 2 года назад
-
10
-
-
Добавить свой ответ
- ДОПОМОЖІТЬ!!!!!4. Укажіть формулу основного оксиду: a) Br,01; 6) SiO2; в) Вао; г) WO3.
-
151. Запишіть подані слова в дві колонки дієприкметники та дієприслівники.
Вмебльований, дотліваючий, знаючи, читаючи, вжалений, утворивши, пишучи,
сказавши,
зеленіючий, працюючи, озвучуючий, даруючи, усвідомлюючи, чару-
ючий,
вмираючий, відаючий, зупинивши
-
Предмет:
Українська мова -
Автор:
norawillis - 2 года назад
-
Ответов:
1 -
Смотреть
-
- Матрицы. Высшая математика. Найти линейные комбинации матриц
-
- 4x2 +7x-8; 2) y = x²+3x²-6x + 5; 7.78. 1) y = 3) y = x 3 1 x-2 4) y = X 4 + 4 X даю 60 балл
-
Предмет:
Алгебра -
Автор:
hannahmartin - 2 года назад
-
Ответов:
1 -
Смотреть
-
