ПРОСЬБА НЕ ПИСАТЬ ДОГАДКИ И НЕ СПАМИТЬ!!!! Сколько можете, пожалуйста. Найти производную: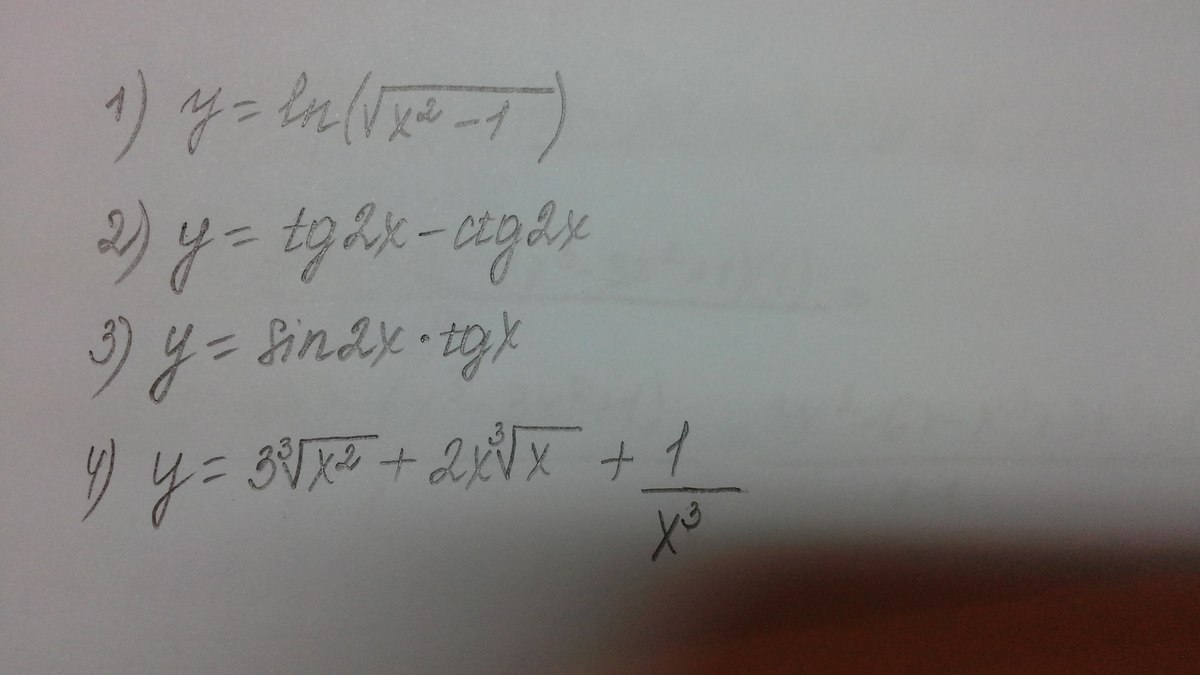

ПРОСЬБА НЕ ПИСАТЬ ДОГАДКИ И НЕ СПАМИТЬ!!!!
Сколько можете, пожалуйста.
Найти производную:
- Предмет:
  Алгебра
- Автор:
  lucyxhoh
- 6 лет назад

Ответы 5

двоечку в последнем примере пропустили
- Автор:
  nicholas4u6h
- 6 лет назад
- 0
это косвенно подтверждает, что решения не списывались друг у друга )))
- Автор:
  pebblesnoble
- 6 лет назад
- 0
ой точно, пропустила))
- Автор:
  alfh4m1
- 6 лет назад
- 0
$1) y= ln( x^{2}-1) ^{ \frac{1}{2} }$ По свойству логарифма степени $y= \frac{1}{2}ln( x^{2} -1)$ $y`= \frac{1}{2} \cdot \frac{1}{ x^{2} -1}\cdot ( x^{2} -1)`= \frac{2x}{2( x^{2} -1)}= \frac{x}{ x^{2} -1}$ $2) y`=(tg2x)`-(ctgx)`= \frac{1}{cos ^{2}2x }(2x)`-( -\frac{1}{sin ^{2}x })= \frac{2}{cos ^{2}2x }+ \frac{1}{sin ^{2}x }$ $3) y`=(sin2x)`tgx+sin2x(tgx)`=2cos2xtgx+ \frac{sin2x}{cos ^{2}x }$ $4) y`=(3x ^{ \frac{2}{3} })`+(2 x^{ \frac{4}{3} })`+( x^{-3})`=3 \cdot\frac{2}{3} x^{ \frac{2}{3}-1 }+2\cdot \frac{4}{3} x^{ \frac{4}{3}-1 }-3x^{-3-1} = \\ = \frac{2}{ \sqrt[3]{x} }+ \frac{8}{3} \sqrt[3]{x} - \frac{3}{ x^{4} }$
- Автор:
  josephfb59
- 6 лет назад
- 0
1) y'=1/√x²-1*2x*1/2√x²-1=x/x²-12) $y'= \frac{2}{ cos^{2}2x }+ \frac{2}{ sin^{2}2x } = \frac{2}{ cos^{2}2x sin^{2}2x }$ 3) $y'=(sin2x)'*tgx+(tgx)'*sin2x=2cos2xtgx+ \frac{sin2x}{ cos^{2}x }$ 4) $y=3 x^{ \frac{2}{3} }+2 x^{ \frac{4}{3} }+ x^{-3}$ $y'= x^{- \frac{1}{3} }+ \frac{8}{3} x^{ \frac{1}{3} }-3 x^{-4}$ $y'= \frac{2}{ \sqrt[3]{x} } + \frac{8}{3} \sqrt[3]{x} - \frac{3}{ x^{4} }$
- Автор:
  rose24
- 6 лет назад
- 0
Добавить свой ответ