-
Решите пожалуйста задачу. Выручайте.
Варианты для СМО с отказами и с ожиданием (65)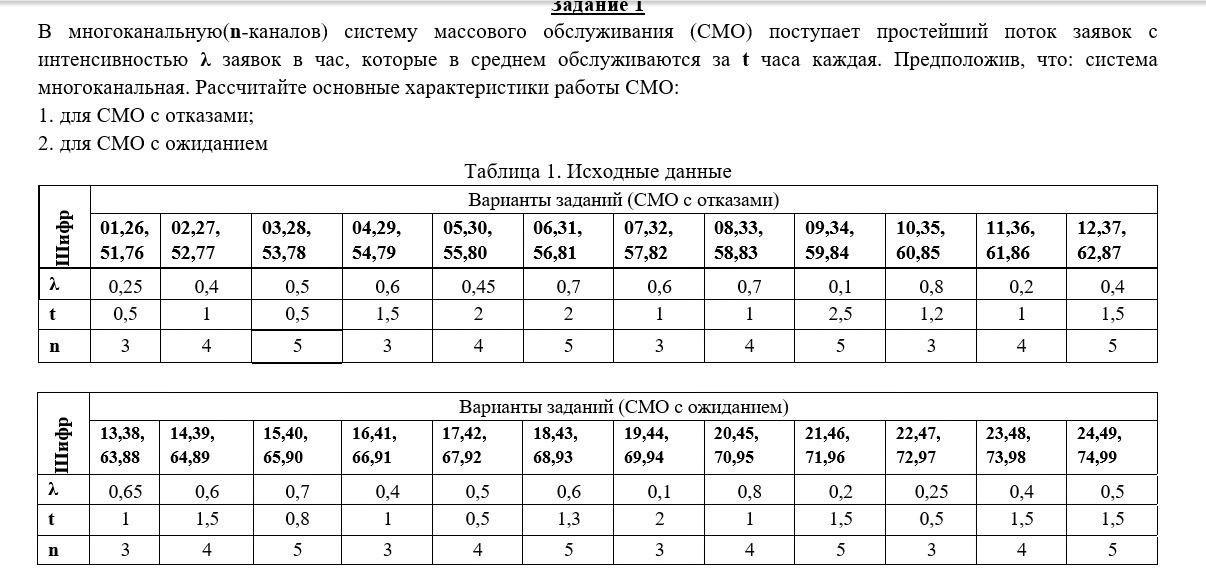
-
Предмет:
Другие предметы -
Автор:
marshmallowyi92 - 6 лет назад
-
Ответы 3
-
Спасибо огромное)))
-
Автор:
kirby52 - 6 лет назад
-
0
-
-
Благодарю
-
Автор:
brock12sz - 6 лет назад
-
0
-
-
65.
Коэффициент использования системы:
Вероятность того, что система свободна:
Среднее число заявок в очереди:
Среднее число заявок в приборе:
Среднее число заявок в системе обслуживания:
Среднее число свободных приборов:
Среднее время ожидания в очереди:
(часов)
-
Автор:
sassiemadden - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
в треугольнике ABC биссектриса BD делит сторону AC в отношении 3 к 2. AB равен 12 см. найдите сторону BC.
-
Предмет:
Математика -
Автор:
benjamin - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Помогите, пожалуйста!!!
Найти [tex] log_{ab} \frac{ \sqrt[3]{a} }{b} [/tex] если [tex]log_{ab}a[/tex]=4-
Предмет:
Математика -
Автор:
joshua - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Розвяжіть задачу: а) Скільки кілограмів солі міститься у 13 кг 8%-го розчину? б) Скільки солі треба розмішати у 5 л води, щоб отримати 5%-й розчин солі?
-
Предмет:
Математика -
Автор:
oliver19 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
(х-1)(х-3)(х-4)(х-6)+10>0. Доказать. В прошлый раз я перепутал условие, прошу прощение у тех, кто думал
-
Предмет:
Алгебра -
Автор:
frederickxxlp - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
