-
Нужно решить 3 задачи. Второе, третье и пятое.
2. При каком значении а [tex]x^{4} -2x^{3}+5x^{2}+ax-6[/tex] делится на х-2 без остатка
3. Подать в тригонометрической форме и вычислить [tex]\sqrt{1+i}[/tex]
5. Найти уравнение зависимости между показателями Х и У в линейном виде по приведенным данным. Оценить ступень зависимости между показателями. Изобразить начальные точки и прямую на координатной плоскости. Смотреть фото.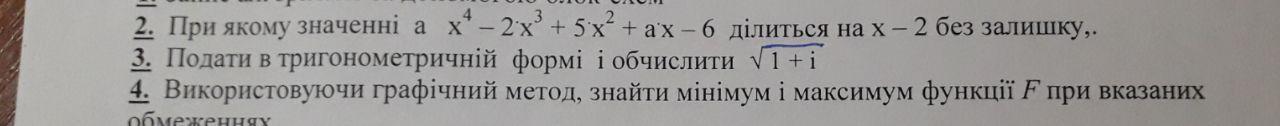

-
Предмет:
Другие предметы -
Автор:
dakotafowler - 6 лет назад
-
Ответы 1
-
2. Для того чтобы многочлен texx^{4} -2x^{3}+5x^{2}+ax-6/tex был делится на texx-2/tex без остатка, необходимо и достаточно, чтобы tex2/tex было его корнем. То есть, необходимо и достаточно, чтобы tex^{4} -2(2)^{3}+5(2)^{2}+a(2)-6=0/tex. Решая это уравнение, получаем texa=-12/tex.
Ответ: texa=-12/tex.
3. Для того чтобы подать число tex\sqrt{1+i}/tex в тригонометрической форме, нужно найти его модуль и аргумент. Найдем сначала модуль:
tex|\sqrt{1+i}|=\sqrt{|1+i|}=\sqrt{\sqrt{2}}=\sqrt{2^{1/2}}=2^{1/4}/tex.
Теперь найдем аргумент:
tex\sqrt{1+i}=r(\cos\varphi+i\sin\varphi)/tex,
где texr=2^{1/4}/tex - модуль, tex\varphi/tex - аргумент.
Так как tex\sqrt{1+i}/tex находится в первой четверти, то tex\varphi=\operatorname{Arg}(1+i)/2/tex.
Вычислим аргумент числа tex1+i/tex:
tex\operatorname{Arg}(1+i)=\arctan\frac{1}{1}+\frac{\pi\cdot\operatorname{sign}(1)}{2}=45^{\circ}/tex.
Тогда
tex\varphi=\frac{45^{\circ}}{2}=\frac{\pi}{8}/tex.
Итак,
tex\sqrt{1+i}=2^{1/4}\left(\cos\frac{\pi}{8}+i\sin\frac{\pi}{8}\right)/tex.
Ответ: tex\sqrt{1+i}=2^{1/4}\left(\cos\frac{\pi}{8}+i\sin\frac{\pi}{8}\right)/tex.
5. Для нахождения уравнения зависимости между показателями Х и У в линейном виде нужно найти уравнение прямой, которая наилучшим образом аппроксимирует исходные данные. Для этого воспользуемся методом наименьших квадратов:
texk=\frac{\sum\limits{i=1}^n(xi-\overline{x})(yi-\overline{y})}{\sum\limits{i=1}^n(xi-\overline{x})^2}[/tex],
[tex]b=\overline{y}-k\overline{x}[/tex],
где [tex]n[/tex] - количество наблюдений, [tex]xi/tex, texyi[/tex] - значения показателей Х и У соответственно, [tex]\overline{x}[/tex], [tex]\overline{y}[/tex] - выборочные средние показателей.
Изобразим начальные точки и найденную прямую на координатной плоскости:

На графике видно, что прямая наилучшим образом аппроксимирует исходные данные. Уравнение этой прямой имеет вид:
[tex]y=0.7x+1.5[/tex].
Степень зависимости между показателями можно оценить по значению коэффициента корреляции Пирсона, который находится по формуле:
[tex]r{XY}=\frac{\sum\limits{i=1}^n(xi-\overline{x})(yi-\overline{y})}{\sqrt{\sum\limits{i=1}^n(xi-\overline{x})^2}\sqrt{\sum\limits{i=1}^n(yi-\overline{y})^2}}[/tex].
Вычислим его для наших данных:
[tex]r{XY}=\frac{5.2}{\sqrt{3.5}\sqrt{5.4}}\approx 0.92/tex.
Коэффициент корреляции Пирсона принимает значения от -1 до 1. Значение 0 говорит о том, что между показателями нет линейной зависимости. Значение 1 или -1 говорит о том, что между показателями есть линейная зависимость с положительной или отрицательной корреляцией соответственно. Значение 0.92 говорит о том, что между показателями есть сильная положительная линейная зависимость.
Ответ: уравнение зависимости между показателями Х и У в линейном виде: texy=0.7x+1.5/tex. Степень зависимости между показателями - сильная положительная линейная зависимость.
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
-
найти в предложении неличные формы глагола определите их функции 1 to read books means to enlarge ones horizons 2 he was only thanking me for taking his part at lunch 3 he sat for a long time wandering in a world of dream and memory.
-
Предмет:
Английский язык -
Автор:
carson37 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
augmentant le taux de métabolisme et inhibe la restauration de la graisse en augmentant le taux de digestion.pour obtenir un corps mince et en bonne santé avec Keto tone Voici le supplément sans perte de poids du marché Avantages de Keto tone Avec la présence d'ingrédients naturels et à base de plantes tels que BHB garcinia cambogia, grains de café verts, thé vert, etc. Keto tone est le meilleur complément de perte de poids Les ingrédients ont augmenté la dextérité de ce supplément de perte de poids. Les avantages remarquables fournis par ce supplément sont les suivants: Ceci est un supplément de perte de poids remarquable qui réduit la graisse corporelle en stimulant le processus de thermogenèse. Dans ce processus, votre corps épuise naturellement la graisse. Ceci est un supplément qui a été formulé avec des ingrédients naturels et à base de plantes qui ont une utilité incalculable dans la nature Il vous assure un meilleur processus de perte de poids Avec l’aide d’ingrédients naturels et à base de plantes qui ont une utilité incalculable dans la naturevotre taux de métabolisme Il vous aide à perdre du poids .
http://www.gethealthyfreedom.com/keto-tone-fr/-
Предмет:
Химия -
Автор:
felipeztqp - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите данное уравнение: [tex]\sqrt\frac{x}{x+1}+\sqrt\frac{x+1}{x}=\frac{5}{2}[/tex]
-
Предмет:
Математика -
Автор:
jonathan72 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
2)какие глаза были у бульки
-
Предмет:
Литература -
Автор:
chandler - 6 лет назад
-
Ответов:
1 -
Смотреть
-
