Задать вопрос Регистрация
Помочь другим

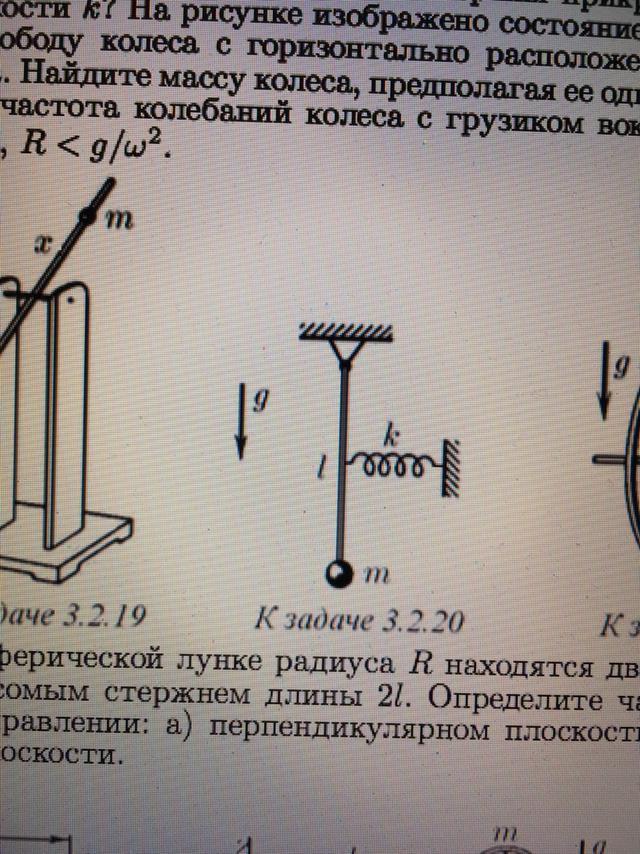
  • Как изменится частота колебаний маятника, представляющего собой груз на легком стержне, если к середине стержня прикрепить горизонтальную пружину жесткости k? На рисунке изображено состояние равновесия.

    question img

Ответы 3

  • прошу прощение за мою не просвещённость,но как это расшифровать?

    • Автор:

      juneb5li
    • 4 года назад
    • 0
  • всё, у меня отобразилось, спасибо))
  • Обобщенной координатой будет угол. Плюс мы сразу ограничимся случаем малых колебаний, так что удлинение пружины мы запишем как L/2*φ. Запишем полную энергию системы:E = mL^2\dot\varphi^2/2 + mgL(1-\cos\varphi) + \frac{1}{2}k\frac{L^2\varphi^2}{4} = const\\\\ E = mL^2\dot\varphi^2/2 + 2mgL\frac{\varphi^2}{4} + \frac{1}{2}k\frac{L^2\varphi^2}{4} = mL^2\dot\varphi^2/2 + (2mgL+\frac{kL^2}{2})\frac{\varphi^2}{4}Продифференцируем по времени\displaystyle 0 = mL^2\dot\varphi\ddot\varphi + (2mgL+\frac{kL^2}{2})\frac{\varphi\dot\varphi}{2} = mL^2\dot\varphi\left(\ddot\varphi+\left(\frac{g}{L}+\frac{k}{4m}ight)\varphiight)В скобках получилось уравнение колебаний, откуда мы понимаем, что новая частота\displaystyle \omega = \sqrt{\frac{g}{L}+\frac{k}{4m}}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years