Два точечных тела с одинаковой массой m каждого подвешены к одной точке на нитях длиной L. сначала нити были разведены и на первое тело помещен заряд q1, а на втором создан избыток в N2 электронов, при этом заряд второго тела стал равен q2. После освобождения тел они притянулись и соприкоснулись, их заряды стали равны q. Затем нити разошлись на угол А, а расстояние между зарядами стало r.

q1нКл = ?
N2 * 1E10 =?
q2 нКл = -112
qнКл = - 46
L = ?
m мг = ?
А град = 44
r см = 44,9

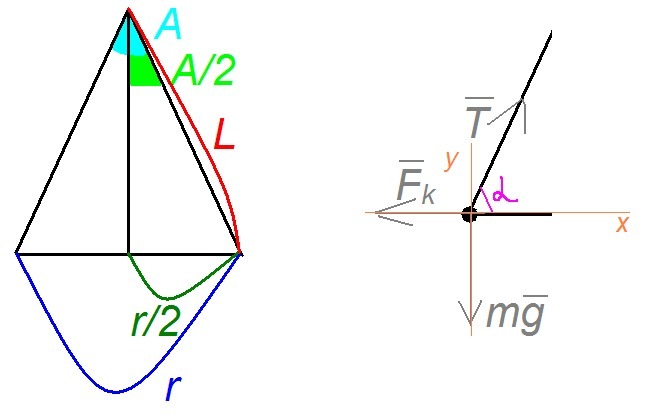
Дано:q₂=-112нКл=-112·10⁻⁹Клq=-46нКл=-46·10⁻⁹КлA=44°r=44.9см=44.9·10⁻²мНайти:q₁, N₂, L, m - ?Решение:Заряд равен произведению заряда одного электрона на их количество:|q_2|=|e|N_2 \\\ N_2= \dfrac{|q_2|}{|e|}Выражаем и находим число электронов:N_2= \dfrac{112\cdot10^{-9}}{1.6\cdot10^{-19}} =7\cdot10^{11}После соприкосновения аров их заряд стал одинаковым и равным среднему арифметическому исходных зарядов:q= \dfrac{q_1+q_2}{2} Величина первого заряда:q_1=2q-q_2 \\\ q_1=2\cdot(-46)-(-112)=20(nKl)После расхождения нити образуют равнобедренный треугольник (на картинке), проведя биссектрису в котором можно записать выражение для синуса:\sin \frac{A}{2} = \dfrac{ \frac{r}{2} }{L} Тогда, длина нити:L= \dfrac{ r}{2\sin \frac{A}{2} } \\\ L= \dfrac{ 44.9\cdot10^{-2}}{2\sin22^\circ } \approx0.6(m)Также, на каждый из двух шариков будут действовать силы: тяжести, Кулона и натяжения нити (на картинке). Так как шарики находятся в покое, то их векторная сумма равна нулю:m\vec{g}+\vec{F_K}+\vec{T}=0Проецируя выражение на пару осей, получим:y: \ mg=T\sin \alpha \\\ x: \ F_K=T\cos \alpha Разделим почленно первое равенство на второе и выразим m: \dfrac{mg}{F_K} =\mathrm{tg} \alpha \\\ m= \dfrac{F_K\mathrm{tg} \alpha }{g} Угол  \alpha =90^\circ- \frac{A}{2} , так как в сумме пара углов при основании составляет 180^\circ-AОпределяем силу Кулона:F_K=k \dfrac{|q|^2}{r^2} \\\ F_K=9\cdot10^9\cdot \dfrac{|-46\cdot10^{-9}|^2}{(44.9\cdot10^{-2})^2} \approx 9.45\cdot 10^{-5}(N)Определяем m:m= \dfrac{9.45\cdot 10^{-5}\cdot\mathrm{tg} (90^\circ- 22^\circ) }{9.8}\approx23.87\cdot10^{-6}(kg)=23.87(mg)Ответ: q₁=20нКл, N₂=7·10¹¹, L=0.6м, m=23.87мг