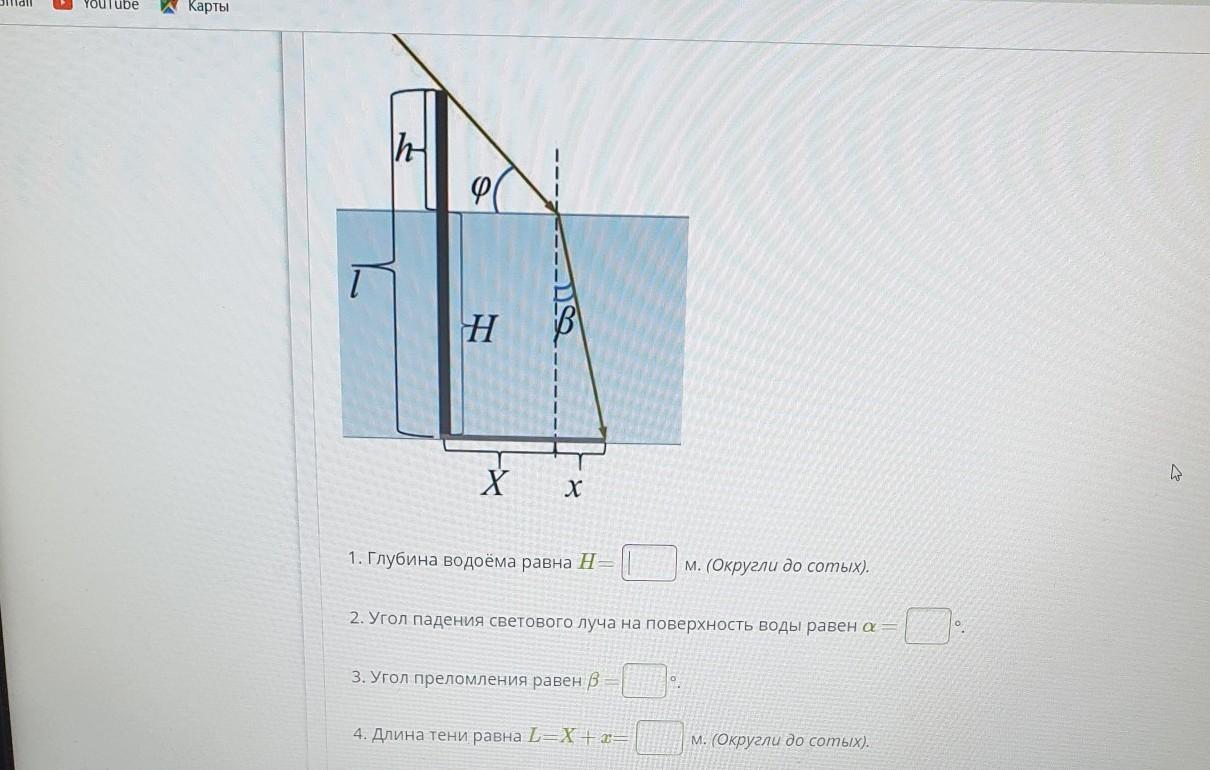
ДАМ 100 БАЛОВ!!!!! ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!! СРОЧНО ОЧЕНЬ НУЖНО Реши поэтапно задачу. Железобетонная опора для моста находится в воде, причем высота возвышения опоры над поверхностью озера равна h=0,38 м, длина всей опоры — L= 1,9 м . Рассчитай длину тени на дне озера от опоры, если показатель преломления воды равен n- √3, угол между падающими на поверхность озера солнечными лучами и горизонтом - ф - 30°.

Ответ:

1.87 метра.

Объяснение:

Для решения задачи воспользуемся геометрическими соображениями и законами оптики.

Рисуем схему: опора моста находится в воде, а над поверхностью озера выступает на высоту h=0,38 м. Из опоры идет луч света под углом ф=30° к поверхности воды, который ломается внутри воды и продолжает свой путь в направлении дна озера. Закон преломления света гласит, что отношение синусов углов падения и преломления равно показателю преломления среды: sin(угол падения) / sin(угол преломления) = n.

Обозначим длину тени на дне озера как x. Тогда по теореме Пифагора в прямоугольном треугольнике, образованном лучом света, его ломанью на границе воздух-вода и вертикальной линии из опоры, получаем:

x^2 + h^2 = L^2

Решим это уравнение относительно x:

x^2 = L^2 - h^2

x^2 = (1.9 м)^2 - (0.38 м)^2

x^2 = 3.504 м^2

x = √3.504 м

x ≈ 1.87 м

Таким образом, длина тени на дне озера от опоры моста составляет примерно 1.87 метра.