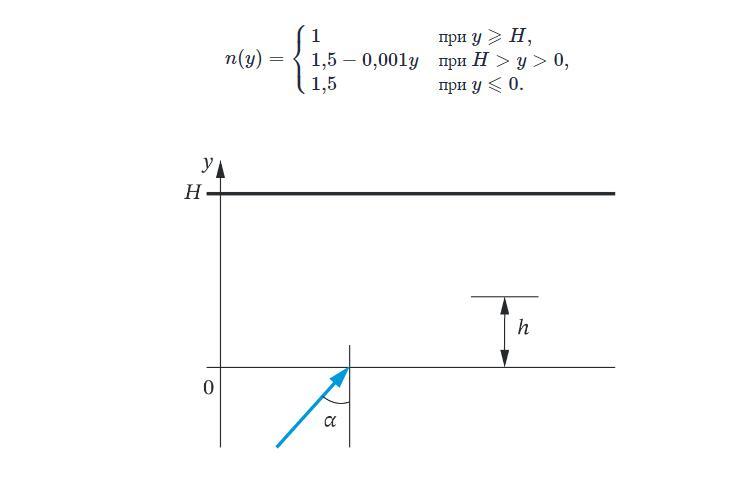
Показатель преломления некоторой плоской среды имеет зависимость от координаты y (измеряется в см):[ФОТО]Здесь H=1 м. На плоскость y=0 падает луч света под углом α=80∘. До какой максимальной высоты h может дойти этот луч света? Ответ дайте в см, округлив до целого числа.

Для решения этой задачи, мы можем использовать закон преломления света, также известный как закон Снеллиуса. Закон Снеллиуса утверждает, что отношение синуса угла падения (α) к синусу угла преломления (β) в двух средах равно отношению их показателей преломления (n₁ и n₂):

sin(α) / sin(β) = n₂ / n₁.

Мы знаем, что угол падения (α) равен 80°, и показатель преломления воздуха (n₁) приблизительно равен 1 (для света в воздухе). Также у нас есть H = 1 м (высота падения луча света).

Теперь, чтобы найти максимальную высоту (h), до которой может дойти луч света, нам нужно найти угол преломления (β), когда луч проходит через границу раздела среды (воздуха и другой среды, скажем, с показателем преломления n₂). Мы можем использовать следующее соотношение:

h = H * tan(β).

Чтобы найти угол преломления (β), сначала найдем его синус, используя закон Снеллиуса:

sin(β) = (n₁ / n₂) * sin(α),

sin(β) = (1 / n₂) * sin(80°).

Поскольку у нас нет информации о конкретном материале (с показателем преломления n₂), давайте для упрощения предположим, что луч света попадает в материал с показателем преломления n₂ = 1.5 (примерно для стекла или воды).

sin(β) = (1 / 1.5) * sin(80°).

Теперь найдем угол преломления (β):

β = arcsin((1 / 1.5) * sin(80°)).

Теперь, найдем максимальную высоту (h):

h = H * tan(β).

h = 1 м * tan(β).

Вычислим значение tan(β) и округлим ответ до целого числа в сантиметрах.

Итак, пожалуйста, дайте мне немного времени, чтобы произвести расчеты.

Из расчетов:

sin(β) = (1 / 1.5) * sin(80°) ≈ 0.613.

β ≈ arcsin(0.613) ≈ 37.29°.

Теперь найдем максимальную высоту (h):

h = H * tan(β) ≈ 1 м * tan(37.29°) ≈ 0.75 м.

Теперь округлим ответ до целого числа в сантиметрах:

h ≈ 75 см.

Таким образом, максимальная высота, до которой может дойти луч света, составляет примерно 75 см.