Помогите, пожалуйста!

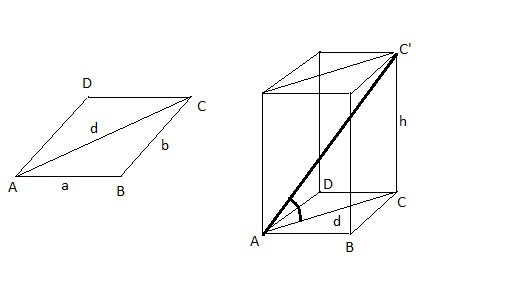
Стороны основания прямого параллелепипеда равны 1 см и 3 см, а синус угла между ними `sqrt5 /3`. Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно `sqrt(14)` см. 

sin A = √5/3; cos^2 A = 1 - sin^2 A = 1 - 5/9 = 4/9; cos A = √(4/9) = 2/3A = arccos(2/3) ~ 48 градусов, это острый угол.cos B = cos(180 - A) = -cos A = -2/3По теореме косинусов в треугольнике АВС в основанииd^2 = a^2 + b^2 - 2ab*cos BЗдесь d - это диагональ основания, a и b - стороны основания.d^2 = 1^2 + 3^2 - 2*1*3*(-2/3) = 1 + 9 + 4 = 14d = √14 - это длина диагонали основания. h = √14 - боковое ребро.Все это нарисовано на левом рисунке.Диагональ основания, боковое ребро и большая диагональ пар-педа образуют прямоугольный треугольник. Так как d = h, то этот прямоугольный треугольник к тому же равнобедренный.Угол между большой диагональю AC' и диагональю основания АС = 45 гр.Это нарисовано на правом рисунке.