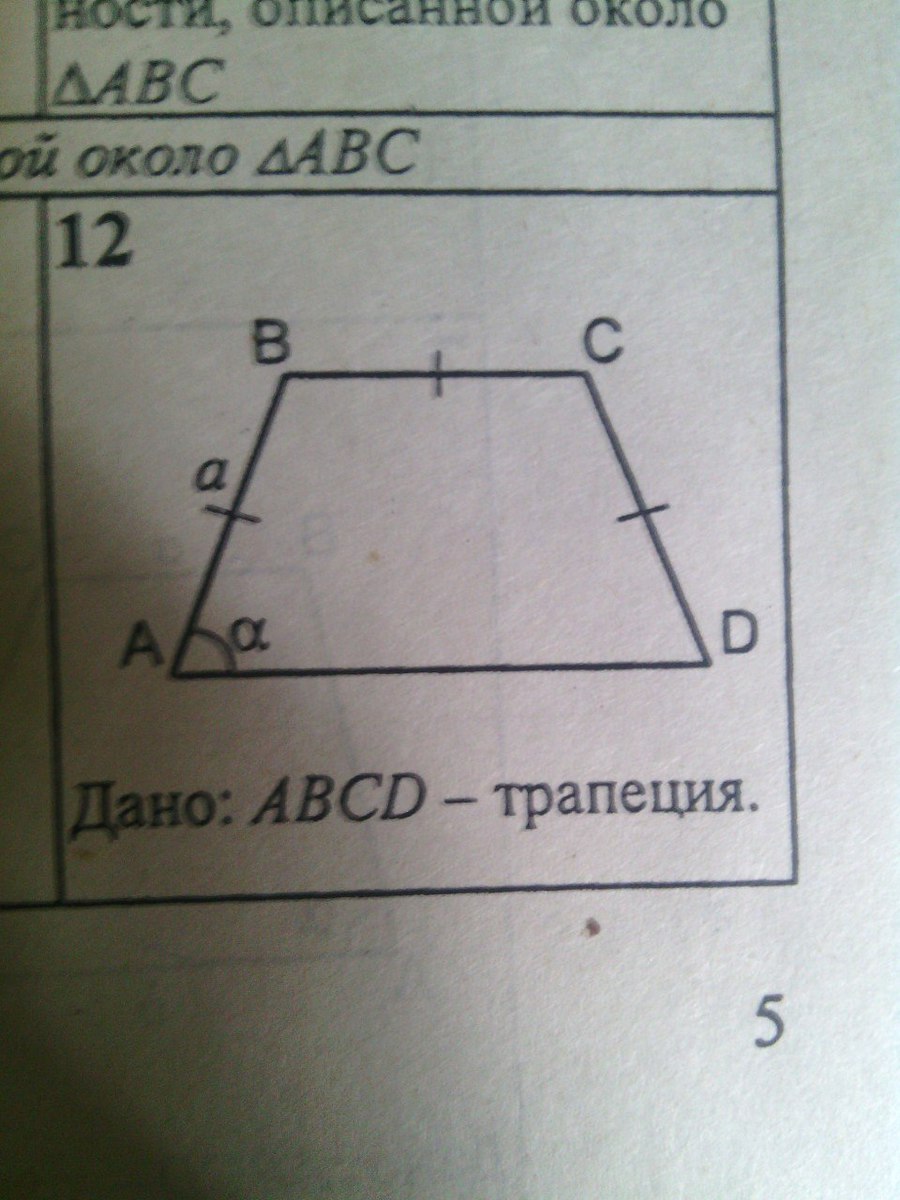
Найти радиус окружности, описанной около треугольника АВС

В равнобедренной трапеции  АВСD боковые стороны и меньшее основание равны. Острый угол А равен α. Найти радиус окружности, описанной около треугольника АВС. --Трапеция равнобедренная, следовательно, вокруг нее можно описать окружность, и это будет одна и та же описанная окружность и для треугольника АВС. Треугольник АВС - равнобедренный. Угол ВАС=углу ВСА. Но угол ВСА - накрестлежащий с углом САD и равен ему. Следовательно, углы ВАС и САD равны, ⇒ АС - биссектриса и делит угол А на два величиной по α/2Опустим перпендикуляр из вершины В и продолжим до пересечения с окружностью в точке Е. Соединим Е и С. Угол СВЕ - прямой, следовательно, ЕС - диаметр описанной окружности. Вписанный угол ВЕС= вписанному углу ВАС, так как опирается на ту же дугу. Угол ВЕС=α/2 ЕС=2R EC=a:sin0,5αR=(a:sin0,5α):2