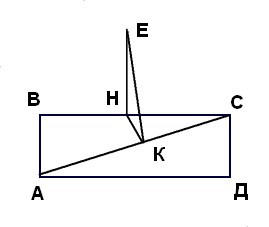
Стороны прямоугольника равны 9 и 12 см. Из середины большей стороны восстановлен перпендикуляр длиной 4,8см к плоскости прямоугольника. Найти расстояние от конца этого перпендикуляра до одной из диагоналей.
Приложите , пожалуйста, рисунок для решения.

Прямоугольник АВСД (АВ=СД=9 и ВС=АД=12)Середина большей стороны - точка Н: (ВН=НС=ВС/2=6)Перпендикуляр ЕН=4,8Нужно найти расстояние ЕК до диагонали АС.Диагональ АС=√(АВ²+ВС²)=√81+144=√225=15Прямоугольные ΔСКН (<CKH=90°) и ΔАДС подобны по острому углу (<НСК=<САД как накрест лежащие при пересечении параллельных прямых ВС иАД секущей АС).Значит НК/СД=НС/АСНК=СД*НС/АС=9*6/15=3,6Из прямоугольного ΔЕНК ЕК=√(ЕН²+НК²)=√(23,04+12,96)=√36=6