-
Задачи и упражнения на готовых чертежах Таблица 7.5 Признаки равнества треугольника
Найти пары равных треугольников и доказать их равенство. ПОМОГИтЕ пожалуйста побыстрей нужно решить все 12.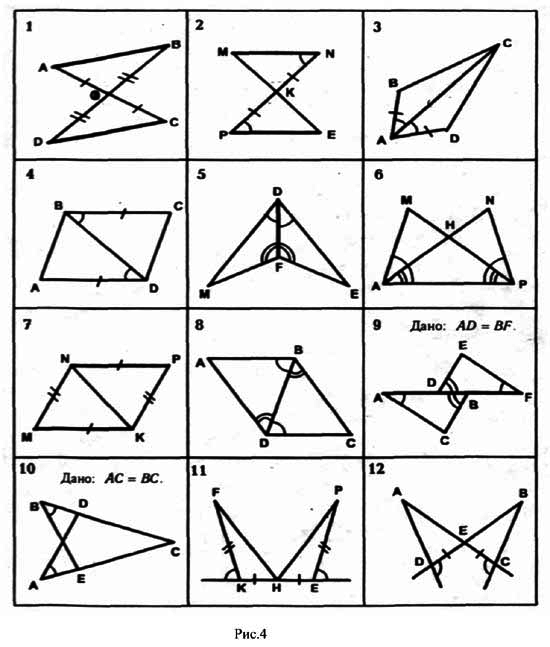
Ответы 2
-
1. АО = ОС, ВО = OD по условию,∠АОВ = ∠COD как вертикальные, ⇒ ΔАОВ = ΔCOD по двум сторонам и углу между ними.2. NK = KP, ∠MNK = ∠EPK по условию,∠MKN = ∠EKP как вертикальные, ⇒ ΔMKN = ΔEKP по стороне и двум прилежащим к ней углам.3. АВ = AD, ∠BAC = ∠DAC по условию,АС - общая сторона для треугольников ABC и ADC, ⇒ΔABC = ΔADC по двум сторонам и углу между ними.4. AD = CB, ∠ADB = ∠CBD по условию,BD - общая сторона для треугольников ADB и CBD, ⇒ΔADB = ΔCBD по двум сторонам и углу между ними.5. ∠MDF = ∠EDF, ∠MFD = ∠EFD по условию,DF - общая сторона для треугольников MDF и EDF, ⇒ΔMDF = ΔEDF по стороне и двум прилежащим к ней углам.6. ∠MAP = ∠NPA, ∠NAP = ∠MPA по условию,АР - общая сторона для треугольников MAP и NPA, ⇒ΔMAP = ΔNPA по стороне и двум прилежащим к ней углам.MA = NP из равенства треугольников MAP и NPA,∠НАР = ∠НРА ⇒ ΔНАР равнобедренный и НА = НР,∠МАН = ∠МАР - ∠НАР∠NPH = ∠NAP - ∠HAP, ⇒ ∠МАН = ∠NPH, ⇒ΔМАН = ΔNPH по двум сторонам и углу между ними.7. МК = PN, MN = PK по условию,NK - общая сторона для треугольников MKN и PNK, ⇒ΔMKN = ΔPNK по трем сторонам.8. ∠ADB = ∠CBD, ∠ABD = ∠CDB по условию,BD - общая торона для треугольников ABD и CDB, ⇒ΔABD = ΔCDB по стороне и двум прилежащим к ней углам.9. ∠CAB = ∠EFD, ∠СВА = ∠EDF по условию,АВ = AD + DBDF = ВF + DB, т.к. AD = BF, то и АВ = DF, ⇒ΔCAB = ΔEFD по стороне и двум прилежащим к ней углам.10. АС = ВС, ∠CAD = ∠CBE по условию,∠АСВ общий для треугольников CAD и CBE, ⇒ΔCAD = ΔCBE по стороне и двум прилежащим к ней углам.11. FK = PE, KH = EH по условию,∠FKH = ∠PEH как углы, смежные с равными углами, ⇒ΔFKH = ΔPEH по двум сторонам и углу между ними.12. DE = CE по условию,∠AED = ∠BEC как вертикальные∠ADE = ∠BCE как углы, смежные с равными углами, ⇒ΔADE = ΔBCE по стороне и двум прилежащим к ней углам.
-
Автор:
baxter5 - 6 лет назад
-
0
-
-
Контрольная работа № 3 по теме: «Второй признак равенства треугольников» (Геометрия, 7 класс)
-
Автор:
easterhath231 - 3 года назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
подберите и запишите существительные, обозначающие состояние, настроение, чувства человека. Определите их род и склонения
-
Предмет:
Русский язык -
Автор:
maia - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Дано n = 5. Определить значение целочисленной переменной S.
-
Предмет:
Информатика -
Автор:
kingqbrp - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Что такое метафора ?Вопрос из блиц турнира по литературному чтению Жар-Птица номер 10 ПОДСКАЖИТЕ ПОЖАЛУЙСТА !
-
Предмет:
Литература -
Автор:
moonshineaqjg - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
НАДО НАЙТИ ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ЕСЛИ ШИРИНА РАВНА 2 СМ А ДЛИННА 5 СМ 5 ММ
-
Предмет:
Математика -
Автор:
smudgechaney - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
