Задать вопрос Регистрация
Помочь другим

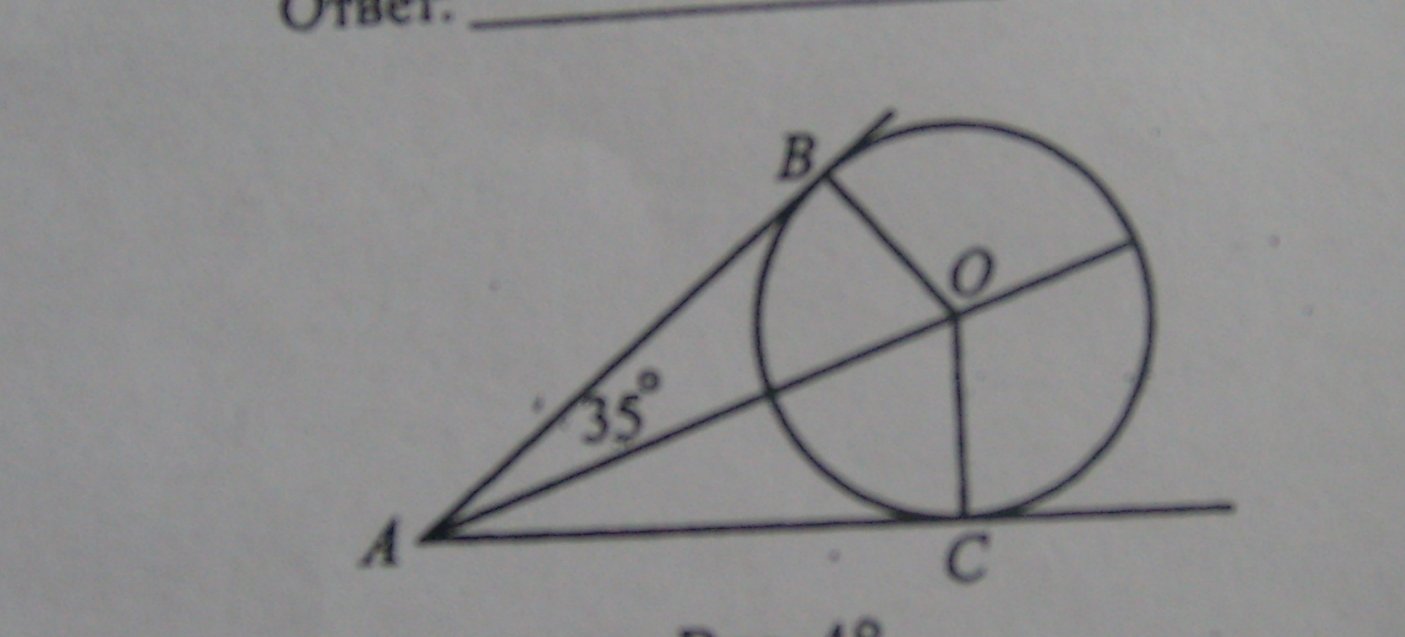
  • прямые АВ и АС касаются окружности с центром в точке О в точках В и С . найдите градусную меру угла ВОС, если угол ВАО=35 градусов. 

    question img

Ответы 1

  • Заметим, что оба треугольника AOB и AOC - прямоугольные. Так как

    \angle ABO=\angle ACO=90^0

     

    как касательные к окружности. Заметим, что эти треугольники равны по трем сторонам. Сторона АО - общая, ВО и ОС - равны как радиусы одной окружности, АВ=АС - как касательные, проведенные к одной окружности из одной точки. Значит

    \angle BOA=\angle COA.

     

    Вычислим угол BOA. По формуле о сумме углов треугольника, получаем

    180^0=\angle BOA+\angle OAB+\angle ABO

    180^0=\angle BOA+35^0+90^0

    \angle BOA=180^0-35^0-90^0

    \angle BOA=55^0

    Так как

    \angle BOC=\angle BOA+\angle AOC

    \angle BOC=2\angle BOA=2*55^0=110^0

    \angle BOC=110^0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years