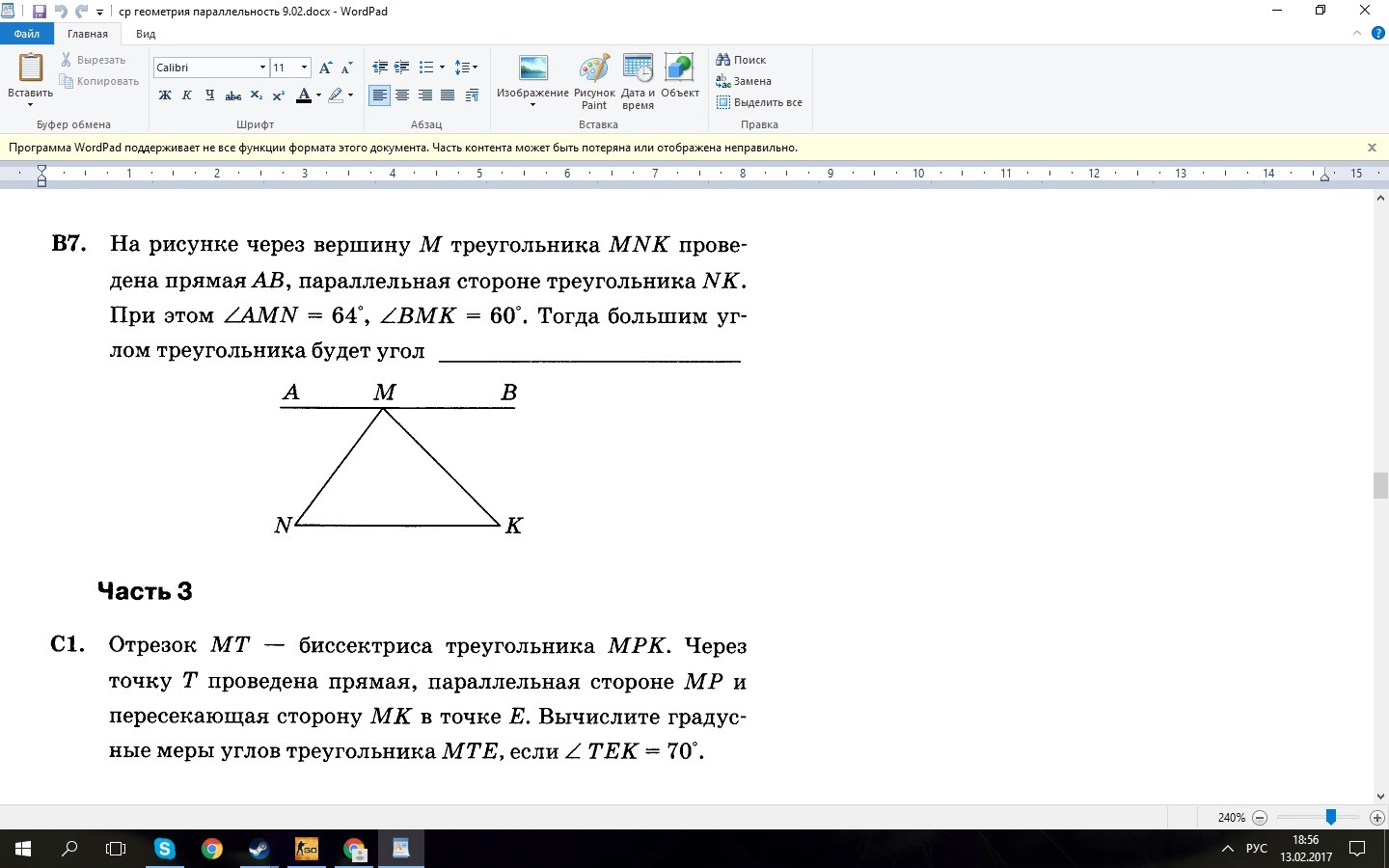
ПОМОГИТЕ ПЛИЗ РЕШИТЬ НОМЕРА B7 И C4 ( С РЕШЕНИЕМ!) ДАЮ 50 БАЛЛОВ

B7.Найти: больший угол треугольника.Решение:∠AMN+∠NМК+∠BMK=180°.∠MNK=∠AMN=64° (как накрестлежащий при параллельных прямых АВ и NK и секущей NМ).∠MKN=∠BMK=60° (как накрестлежащий при параллельных прямых АВ и NK и секущей МK).∠NМК=180-(64+60)=56°. Ответ: ∠MNK - больший угол треугольника.  С1. Найти: ∠МЕТ, ∠МТЕ, ∠ТМЕ.Решение: Рассмотрим треугольник МРК. В нем МТ - биссектриса, следовательно ∠РМТ=∠КМТ. ТЕ параллельна МР  и ∠ТЕК=70°, значит ∠ТЕМ=180-70=110° (∠ТЕК и ∠ТЕМ - смежные углы и их сумма равна 180°).Т.к. ТЕ параллельна МР, а  МТ - секущая, то ∠ РМТ=∠ АТМ (как накрест лежащие при параллельных прямых ТЕ и МР и секущей МТ).Треугольник МТЕ - равнобедренный, т.к. ∠РМТ=∠КМТ (МТ - биссектриса)  и ∠МТЕ=∠РМТ (как накрест лежащие углы). Следовательно ∠МТЕ=∠ТМЕ=(180-110)/2=70/2=35.  Ответ: ∠МЕТ=110°, ∠МТЕ=35°, ∠ТМЕ=35°.