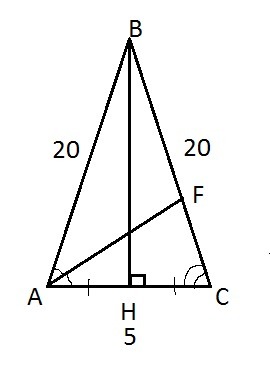
основа рівнобедреного трикутника дорівнює 5 см а бічна сторона 20 знайдіть бісектрису кута проведену з вершини кута при його основі

1) Пусть ΔАВС - равнобедренный, АВ=ВС=20 см, АС=5 см. Проведём биссектрису AF и высоту ВН.2) По свойству биссектрисы BF/FC=AB/AC=20/5=4;BF/FC=4;BF=4FC;FC=x, BF=4x;BC=BF+FC=4x+x=5x=5FC.20=5FC;FC=20/5=4 (cм).3) Рассмотрим ΔВНС - прямоугольный, ВС=20 см, НС=1/2НС=1/2*5=5/2 (см).cosC=HC/BC=5/2:20=5/2*1/20=1/8.4) Рассмотрим ΔAFC, по т.косинусов находим биссектрису AF:AF²=AC²+FC²-2*AC*FC*cosC;AF²=5²+4²-2*5*4*1/8=25+16-5=36;AF=6 (cм).Ответ: 6 см.Биссектрису треугольника можно еще найти по формуле: l_{a}= \frac{\sqrt{bc(a+b+c)(b+c-a)}}{b+c} , где a, b, c - стороны треугольника.AF= \frac{\sqrt{AC*AB(BC+AC+AB)(AC+AB-BC)}}{AC+AB}= \frac{\sqrt{5*20(20+5+20)(5+20-20)}}{5+20}= \\ =6