-
помогите сделать 5 и 6
тема : параллельные прямые 7 класс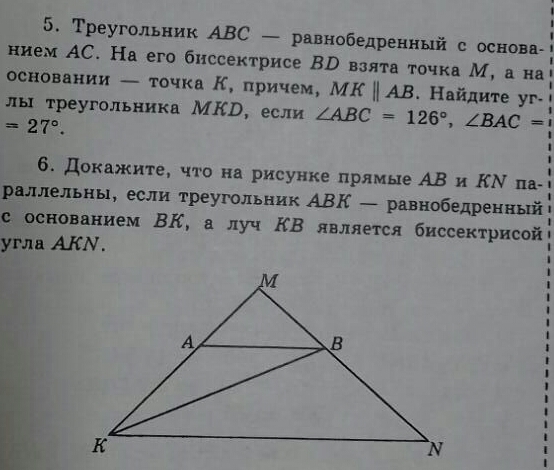
Ответы 2
-
Спасибо большое
-
Автор:
hildegarda - 5 лет назад
-
0
-
-
№5. Треугольник АВС – равнобедренный с основанием АС. На его биссектрисе ВD взята точка М, а на основании – точка К, причем МК||АВ. Найдите углы треугольника МКD, если угол АВС=126°, угол ВАС=27°
МК ║ АВ При пересечении параллельных прямых секущей соответственные углы равны. ⇒
∠МКD=∠ВАС=27°
Биссектриса равнобедренного треугольника, проведенная между равными сторонами, является его высотой. Следовательно, ∠ BDK=90°
∠КМD=180°-90°-27°=53°
Углы ∆ МКD равны 27°, 90°, 53° (Величина угла АВС для решения оказалась лишней).
---------------
№6. Докажите, что на рисунке прямые АВ и KN параллельны, если треугольник АВК –равнобедренный с основанием ВК, а луч КВ является биссектрисой угла АКN. , что на рисунке прямые АВ и КN (См. рисунок)
По свойству углов при основании равнобедренного треугольника ∠АВК=∠ВКА.
Так как КВ - биссектриса, то ∠АКВ=∠ВКN.
Но угол АКВ=АВК. ⇒
Накрестлежащие углы АВК и ВКN равны.
Равенство накрестлежащих углов при пересечении двух прямых секущей - признак параллельности этих прямых. ⇒
АВ║KN, ч.т.д.

-
Автор:
irisleon - 5 лет назад
-
0
-
-
Добавить свой ответ
-
ПОЖАЛУЙСТА ПОМОГИТЕ СРОЧНО НУЖНО
1. заполните пропуски:
A female person whose spouse has died and who has not married again is called....
A) a widower
B) an ex-wife,
C) a Widow
D) an ex-husband
2. Заполните пропуски
She'd better.... Her bus leaves at 7.30.
A) hurry
B) to hurry
C) hurrying
D) to hurrying
3. Заполните пропуски
Someone who is related to you and who lived a long time ago is called....
A) a descendant
B) a child
C) an ancestor
D) a a tsar
4.заполните пропуски
You shouldn't hit....
this employee. Your criticism is unfair
A) on,
B) out:
C) up;
D) for
5. Заполните пропуски
If he.... this song 2 years ago, he..... part in the yesterday Concert
A) composed: would take
B) composed: would have taken
C) would have composed: had taken
D) had composed, Would have taken
6. Выберите слово, НЕ являющееся синонимом для остальных:
A) stunning:
B) striking
C) surprising
D) sensible
7. Заполните пропуски
.... - strange and unusual, sometimes in a way that upsets you.
A) lively
B) weird
C) sensitive
b) outgoing
8. Заполните пропуски
The witness saw.... the front door of the bank at 5.30 p. m.
A) he enter
B) him entering
C) he to enter
D) him to entering
9. Выберите слово, НЕ обозначающее архитектурное сооружение
A) mansion
B) chapel
C) achievement
D) castle
10. Заполните пропуск
Their summit must ....... this year
A) to organize
B) be organized
C) organized
D) be organize
11. Заполните пропуск
A sympathetic person is a person.....
A) who Is kind to someone who has a problem
B) who Is very beautiful
C) who has good table manners
D) who Is intelligent
12. Заполните пропуск
Kazan Cathedral...... in St. Petersburg.
A) knows to be
B) is known to be
C) knows be,
D) is known be
13. Заполните пропуски
The monument...... Queen Victoria was erected in front of Buckingham Palace
A) in
B) to
C) for
D) on
14. Выберете слово, к которому можно прибавить приставку dis-:
A) honest
B) believable
C) polite
D) dividedd
15. Заполните пропуск
The BBC reporter said that the G-20 meeting.... in Hangzhou the previous year.
A) had held
B) would be held
c) had been held
D) has been held-
Предмет:
Английский язык -
Автор:
mercedesvega - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Вычислите площадь треугольника АВС
-
Предмет:
Математика -
Автор:
lexicontreras - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
пояснити вислів ніхто не може поліпшити своє становище своїм же правопорушенням
-
Предмет:
Українська мова -
Автор:
lauren3lrm - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите производные функции
[tex]f(x) = {x}^{2} (x + 2) \\ f(x) = {x}^{3} + 2 {x}^{2} + x + 30 \\ [/tex]
[tex]f(x) = \sqrt{4 - 3 {x}^{2} } \\ f(x) = \cos(2 {x}^{2} - 3x + 1 ) [/tex]
