Окружность касается сторон треугольника, длины которых равны 9, 10 и 11. Найдите длину наибольшего из отрезков, на которые точка касания делит сторону, равную 10.

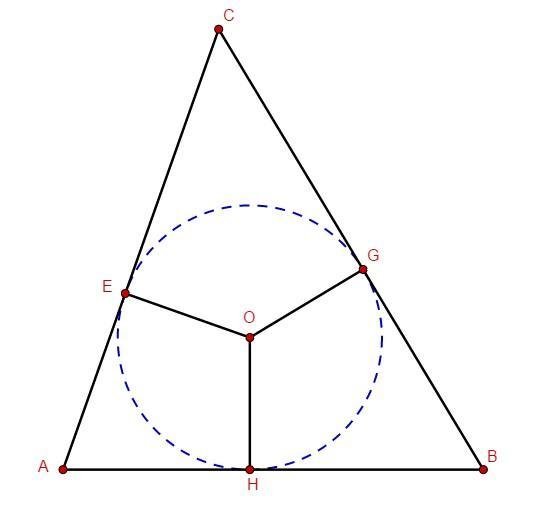
AC = 10; BC = 11; AB = 9.

Пусть CE=x, тогда CE=CG=x (как касательные к окружности). Тогда AE=10-x и BG=11-x. Тогда AE=AH и GB=HB (как касательные к окружности).

AB=AH+HB\\ \\ 9=10-x+11-x\\ \\ 2x=12\\ \\ x=6

Тогда AE = 10 - 6 = 4, откуда наибольший отрезок будет CE = 6

Ответ: 6.