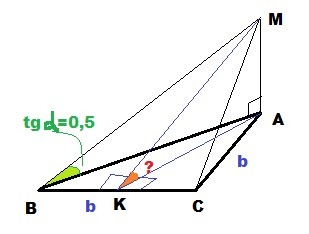
из вершины А правильного треугольника ABC проведен к его плоскости перпендикуляр АМ. Точка М соединена с точками B и C. тангенс угла,образованного стороной МB с плоскостью треугольника ABC,равен 0,5. найдите двугранный угол, образованный плоскостями ABC и MBC

ΔABC :  AB = BC = AC = bAM⊥(ΔABC) ⇒ ∠MAB = ∠MAC = 90°ΔMAB :  ∠MAB = 90°; tg∠MBA = 0,5  ⇒MA = AB*tg∠MBA = 0,5bΔABC : AK⊥BC  ⇒ AK = b*sin60° = b√3/2AB=AC - проекции наклонных на плоскость равны ⇒ равны наклонные  MB = MC  ⇒ΔBMC - равнобедренный  ⇒  MK⊥BC  ⇒∠MKA равен двугранному углу между плоскостями  MBC и ABC.ΔMKA : ∠MAK = 90°; MA = 0,5b;  AK = b√3/2  ⇒tg∠MKA = MA / AK = 0,5b / (b√3/2) =  \frac{0,5b*2}{ b\sqrt{3} } = \frac{1}{ \sqrt{3} }   ⇒∠MKA = 30°Ответ: двугранный угол равен 30°