Общая хорда двух пересекающихся окружностей является стороной правильного треугольника, вписанного в одну окружность, и стороной правильного шестиугольника, вписанного в другую окружеость. Длина этой хорды равна а. Найдите расстояние между центрами окружностей если она лежит по одну сторону от хорды.
Расписать.

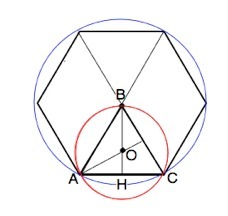
Правильный шестиугольник состоит из 6 правильных треугольников со сторонами, равными данной хорде. т.е. а. Если центры окружностей лежат по одну сторону от данной хорды, а хорда - общая сторона этих многоугольников, то вершина В треугольника АВС совпадает с центром шестиугольника, и расстояние между их центрами равно радиусу окружности, описанной около правильного треугольника ( см. рисунок вложения). ВО=r=а/√3