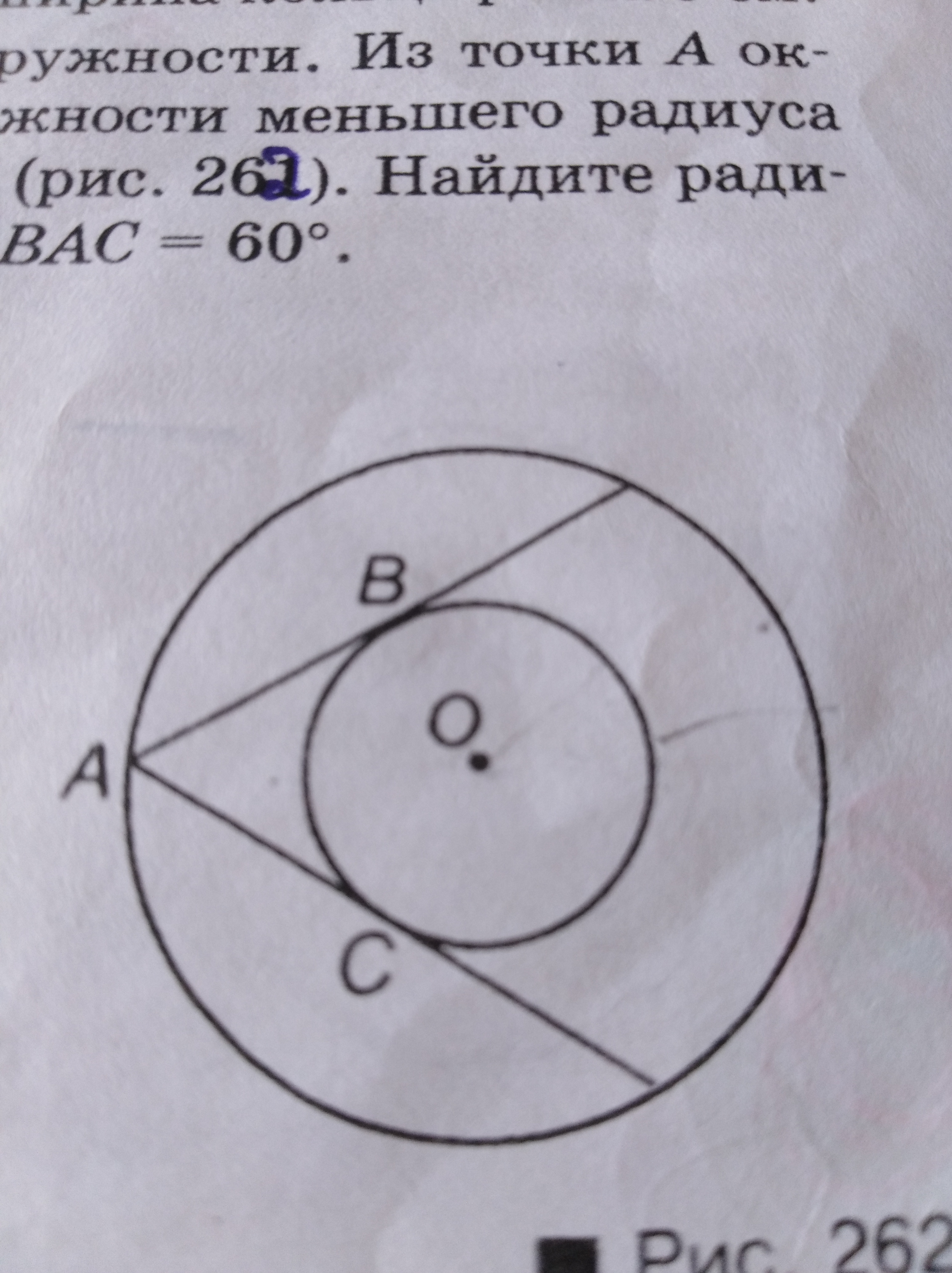
Даны две окружности концентрические. Из точки А окружности радиуса 10см к окружности меньшего радиуса проведены касательные АВ и СД. Найдите радиус меньшей окружности, если угол ВАС=60градусов

Так как АВ и АС - касательные к м'еньшей окружности, то эти отрезки перпендикулярны радиусам м'еньшей окружности , проведённым в точку касания, то есть АВ⊥ОВ , АС⊥ОС , где R=ОВ=ОС .

Радиус б'ольшей окружности равен ОА=10 см.

∠ВAС=60° , АВ=АС как отрезки касательных, проведённых из одной точки

Рассм. ΔАОВ и ΔАОС: ∠АВО=90° , АВ=АС , АО - общая гипотенуза ⇒ ΔАОВ=ΔАОС по гипоненузе и катету ⇒ ∠ВАО=∠САО=∠ВАС:2=60°:2=30° ΔАОВ: ВО - катет, лежащий против угла в 30°, значит он равен половине гипотенузы, то есть ВО=АО:2=10:2=5 .

Но катет ВО - есть радиус меньшей окружности , R=BO=5 см .