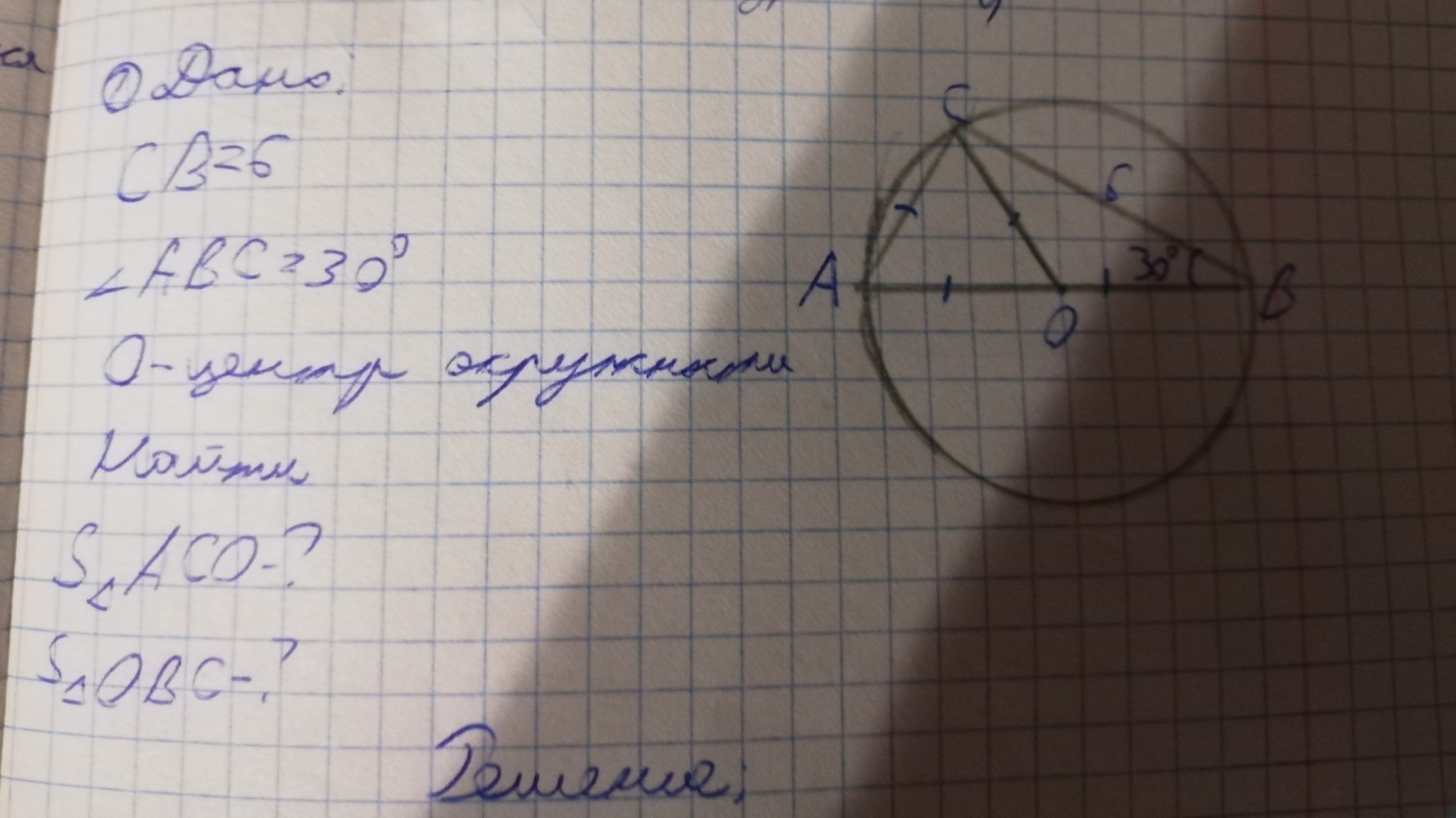
Решите, АС=СО=АО=ОВ, найти площадь треуг АСО и СОВ . С решением

Сначала заметим, что площади треугольников ACO и OBC равны, поскольку у них одна и та же высота (проведенная из вершины С к прямой AB), и основания AO=OB.

Треугольник ACB прямоугольный, поскольку угол С опирается на диаметр описанной около треугольника ACB окружности, то есть <C = 90 градусов.

Пусть AC=x, тогда AB = AO+OB = x+x = 2x. По теореме Пифагора для треугольника ACB имеем

AB² = AC² + BC²,

(2x)² = x² + BC²,  BC = 6 по условию.

4*x² = x² + 6²,

3*x² = 36,

x² = 36/3 = 12

x = √(12) = √(3*4) = 2*√3,

Т.к. треугольник ACB прямоугольный его площадь равна половине произведения его катетов:

S(ACB) = (1/2)*AC*BC = (1/2)*2*(√3)* 6 = 6*√3,

Т.к. площади ACO и OBC равны, то площадь каждого из них равна половине площади ACB, то есть S(ACO) = S(OBC) = S(ACB)/2 = 6*(√3)/2 =

= 3*√3.

Треугольник АВС прямоугольный (АВ диаметр описанной окружности);

угол В=30° ⇒ АВ=2АС;

по т. Пифагора - х²+6²=4х² (АС=х), х=2√3;

площадь АВС=АС*СВ/2=6√3;

медиана в треугольнике делит его на два равновеликих треугольника;

S(АСО)=S(СОВ)=S(АВС)/2=6√3/2=3√3.