-
помогите решить 1,2,3 номер ♥️
тема : Признаки подобия треугольников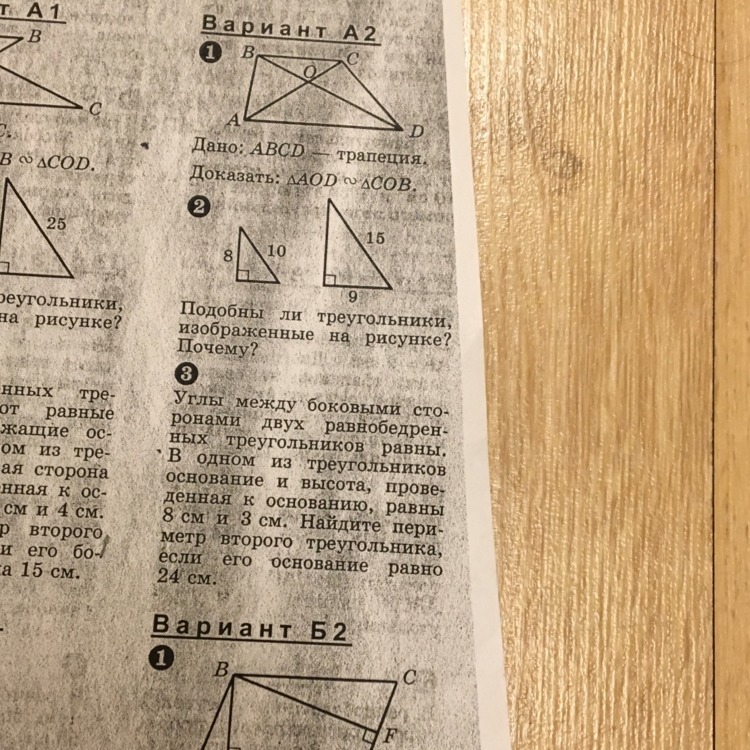
Ответы 6
-
Рад помочь тебе, но с третим заданием то что делать?
-
Автор:
craig78 - 6 лет назад
-
0
-
-
Ау
-
Автор:
joaquinxftv - 6 лет назад
-
0
-
-
Ты чего... 6 минут назад..
-
Автор:
barker - 6 лет назад
-
0
-
-
Ну.... ладно... Потом решу,Вопрос не закрывай=Р
-
Автор:
pugsleyvwsl - 6 лет назад
-
0
-
-
Не удаляй*
-
Автор:
houdiniqqlr - 6 лет назад
-
0
-
-
Задание №1.
Дано:
"ABCD" - трапеция; "" - точка пересечения "AC" и "DB".
Доказать:
Δ"AOD" ∞ Δ"COB".
Доказательство:
Так как в точке"" образуются вертикальные углы, то вполне разумно сказать, что ∠"AOD" = ∠"COB". У нас дана трапеция, а у неё основания параллельны. Сторона "" служит секущей и выходит, что ∠"ADO" = ∠"BOC" как накрест лежащие. Мы доказали равенство двух углов у каждого треугольника, выходит, что Δ"AOD" ∞ Δ"COB" по первому признаку подобия (Два угла у одного треугольника соответственно равны двум углам другого треугольника).
Задание №2.
Дано:
(Для удобства обозначим треугольники)
(маленький) Δ"ABC" и (большой) Δ"DFG"; "AB" = 8 см; "AC" = 10 см; "DG" = 15 см; "FG" = 9 см; ∠"B" = ∠"F" = 90°.
Доказать:
Δ"ABC" ∞ Δ"DFG".
Доказательство:
Найдём сначала коэффициент подобия этих треугольников. Для этого, возьмём известные нам соответственные стороны: "AC" и "DG":
1.
=
.
Возьмём теперь другую пару соответственных сторон и сравним их коэффициент подобия с первой парой, но нам нужно сначала найти сторону "DF":
2. 15^{2} - 9^{2} = 225 - 81 = 144 -> 12 см.
Теперь, сравним наконец коэффициенты:
3.
и
=
и
.
Данное решение является свидетелем того, что эти треугольники равны по второму признаку подобия треугольников (Две стороны соответственно подобны двум сторонам другого и угол между ними равен )
Удачи!

-
Автор:
haileyclark - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Почему в Древней Греции в Олимпийских играх атлеты принимали участие обнажённые?
-
Предмет:
Окружающий мир -
Автор:
zoie99 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как вы думаете почему Андрий при встрече с отцом не промолвил ни единого слова?
(Тарас Бульба)-
Предмет:
Литература -
Автор:
buckyboyd - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
СРОЧНО!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Воздушное питание - это....
1)поглощение углекислого газа и воды
2)выделение кислорода
3)потребление энергии солнца
4) поглощение минеральных веществ-
Предмет:
Биология -
Автор:
aldenmccann - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Будь-ласка розв'яжіть рівняння:
|x| = 0,9
|y| = -5
-a = 4/9-
Предмет:
Математика -
Автор:
junecarson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
