-
Найдите высоту треугольника ABC, опущенную на сторону BC, если стороны квадратных клеток равны 1.
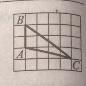
Ответы 3
-
а зачем Герон ? Высота , проведенная к АВ равна 4 , АВ = 2 , S = (4*2)/2
-
Автор:
vegas84 - 6 лет назад
-
0
-
-
Согласен.
-
Автор:
rocky28 - 6 лет назад
-
0
-
-
В треугольнике АВС стороны равны:
АВ = 2,
АС = √(1+4²) = √17 (по Пифагору),
ВС = √(3²+4²) = 5 (тоже по Пифагору.
Полупериметр треугольника АВС равен (7+√17)/2 ед.
Тогда по Герону площадь треугольника АВС равна:
S = √((7+√17)*(√17-3)*(7-√17)*(√17+3))/4 или
Sabc = 16/4 = 4 ед².
С другой стороны Sabc = (1/2)*BC*h =>
h = 2S/ВС = 8/5 = 1,6 ед.
Ответ: высота, опущенная на сторону ВС, равна 1,6 ед.
P.S. для сравнения:
По теореме Пика ( к сожалению, ее в школьной программе нет?) площадь треугольника АВС равна:
S = В + Г / 2 − 1, где В — количество целочисленных точек внутри многоугольника (зеленые точки), а Г — количество целочисленных точек на границе многоугольника (красные точки.
В нашем случае: Sabc= 3+4/2-1= 4 см².

-
Автор:
cocoa - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Помогите!
Определить знак выражения:
cos263градуса ; ctg1364градуса -
эссе на тему " стоили ли люди которых данко вывел на свет , вырванного из груди сердца?" помогите пожалуйста
-
Предмет:
Литература -
Автор:
cutie11 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Помогите, пожалуйста, решить задание по алгебре, прикрепила скрин ниже
-
Вопрос жизни и смерти !
4x^3 - 100x = ?
128y - 2y^3 = ?
^ = степень
(Знаю вопрос тупой) Заранее спасибо-
Предмет:
Математика -
Автор:
helenatrevino - 6 лет назад
-
Ответов:
1 -
Смотреть
-
