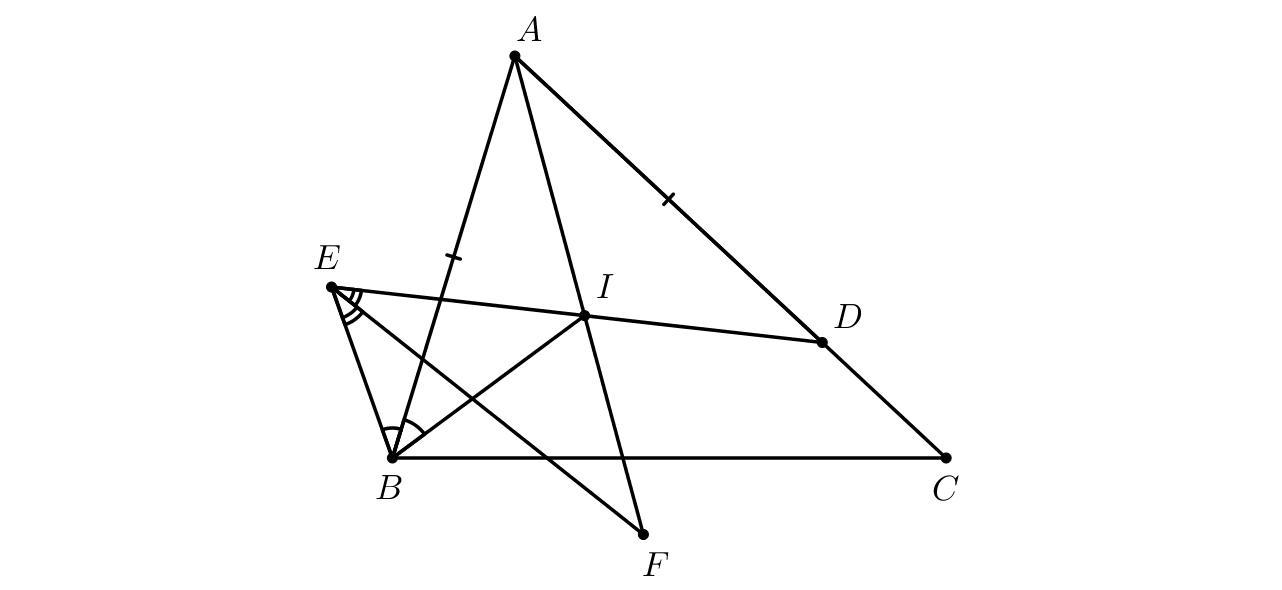
В треугольнике ABC на стороне AC выбрана точка D так, что AB=AD. I — центр вписанной окружности треугольника ABC. На луче DI выбрана точка E такая, что луч BA является биссектрисой угла IBE. Биссектриса угла BEI пересекает прямую AI в точке F. Выберите несколько точек, 3 из которых являются вершинами треугольника, а остальные — его центром (или центрами) вневписанной окружности (окружностей).

Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.

Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC

△BAI=△DAI (по двум сторонам и углу между ними)

∠BIF=∠DIF (смежные с равными)

AF - биссектриса внешнего угла ∠BID треугольника BEI

EF - биссектриса внутреннего угла ∠BEI

F - центр вневписанной окружности △BEI

BA - биссектриса внутреннего угла ∠EBI треугольника BEI

A - центр вневписанной окружности △BEI