-
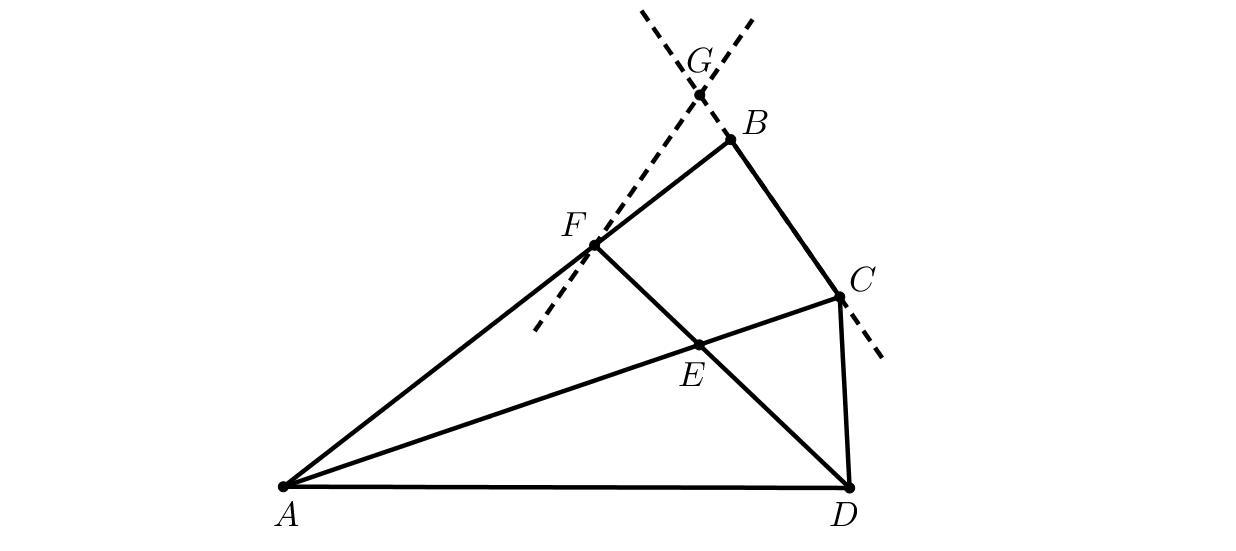
В четырёхугольнике ABCD выполнены равенства AB=AD и BC=CD. Биссектриса угла D пересекает диагональ AC в точке E, а сторону AB — в точке F. Прямая, симметричная AB относительно прямой FD, пересекает прямую BC в точке G. Выберите несколько точек, 3 из которых являются вершинами треугольника, а остальные — его центром (или центрами) вневписанной окружности (окружностей).
-
Предмет:
Геометрия -
Автор:
jamarcuscantu - 6 лет назад
-
Ответы 1
-
Ответ:
Треугольник FGB и точка E - центр вневписанной окружности.
Объяснение:
Заметим для справки, что четырехугольник с такими свойствами как ABCD, называется дельтоидом. Но не в этом суть. В силу того, что этот четырехугольник образован двумя равными треугольниками ABC и ADC, биссектриса угла ABC пересечется со стороной AC в той же точке, что и биссектриса угла ADC, то есть в точке E. Кроме того, из симметричности прямых AB и FG относительно FD, следует равенство углов EFB и EF? (автор задания не удосужился на нужном луче проставить какую-нибудь букву, не делать же мне из-за такой небрежности автора свой чертеж; если бы мой чертеж заранее предполагался, я не стал бы браться за задачу); знак ? нужно нарисовать на луче GF за точкой F. Таким образом, точка E является точкой пересечения двух внешних углов треугольника FGB и тем самым является центром вневписанной окружности, касающейся стороны EB и продолжений сторон FG и BG
-
Автор:
eugenioferguson - 6 лет назад
-
0
-
-
Добавить свой ответ
- В треугольнике ABC на стороне AC выбрана точка D так, что AB=AD. I — центр вписанной окружности треугольника ABC. На луче DI выбрана точка E такая, что луч BA является биссектрисой угла IBE. Биссектриса угла BEI пересекает прямую AI в точке F. Выберите несколько точек, 3 из которых являются вершинами треугольника, а остальные — его центром (или центрами) вневписанной окружности (окружностей).
-
Решите пожалуйста в). а) и б) я решила
1. Камень свободно падает с высоты 80 м.
а) Чему равна скорость камня при падении на поверхность земли?
ответ: V=20 м/с
б) Чему равно время падения?
ответ: 4с
в) Постройте график зависимости модуля скорости от времени. -
найдите критические точки функции
f(x)=x^3-3x+7-
Предмет:
Математика -
Автор:
sirochristensen - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Найти период и частоту колебаний в контуре, емкость конденсатора в котором 2×10-10 Ф, индуктивность катушки 20×10-4 Гн.
