Ответы 1
-
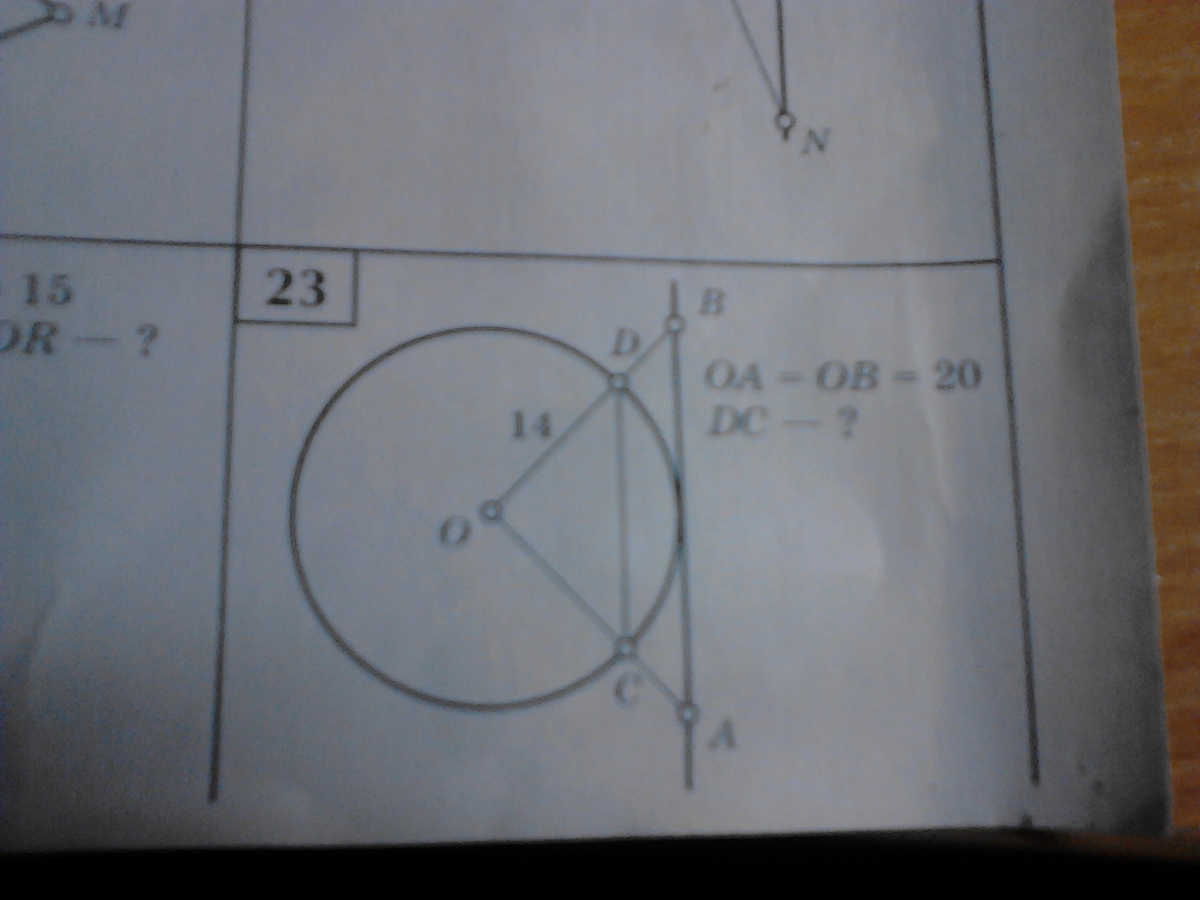
АВ- касательная к окружности с центром О и радиусом 14.
ОА=ОВ=20
С и D - точки пересечения ОА и ОВ с окружностью. Найти CD.
--------------
ОА=ОВ => ∆ АОВ равнобедренный.
Отрезок ОМ, проведеный из О в точку касания, равен r=14 и перпендикулярен АВ ( свойство радиуса к точке касания)=>
ОМ - высота, биссектриса, медиана ∆ АОВ
∆ АОМ прямоугольный.
По т.Пифагора
АМ=√(AO²-OM²)=√(400-196)=2√51 =>
AB=2•AM=4√51
В равнобедренных ∆ АОВ и ∆ СОD угол при вершине О общий, следовательно, углы при основаниях CD и АВ равны. ⇒
∆ АОВ~∆ СОD по равным углам.
Коэффициент подобия k=ОD:ОВ=14:20=0,7
СD=AB•0,7=2,8√51

-
Автор:
rodneyballard - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Расскажите в письме своему товарищу о чём-нибудь интересном:событии,книге,фильме,поедке,покупке,и т.д.
-
Предмет:
Русский язык -
Автор:
oneal - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
нужно пояснение..почему пишется именно с этой буквой
присуТствовать.
почуВствовать
поднявшиЕся
рассеЯлся
завезеННыми
нескОнчаемо
грЕмели
в напрЯженИИ
ножОм,надвОЕ,раСчищать
-
Предмет:
Русский язык -
Автор:
guadalupeortega - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
разность двух натуральных чисел равна 24, а их произведение равно 481.Найдите эти числа.
-
Предмет:
Математика -
Автор:
jethro - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
минеральные вещества клетки ( значение-вещества)
-
Предмет:
Биология -
Автор:
josefamccoy - 6 лет назад
-
Ответов:
0 -
Смотреть
-