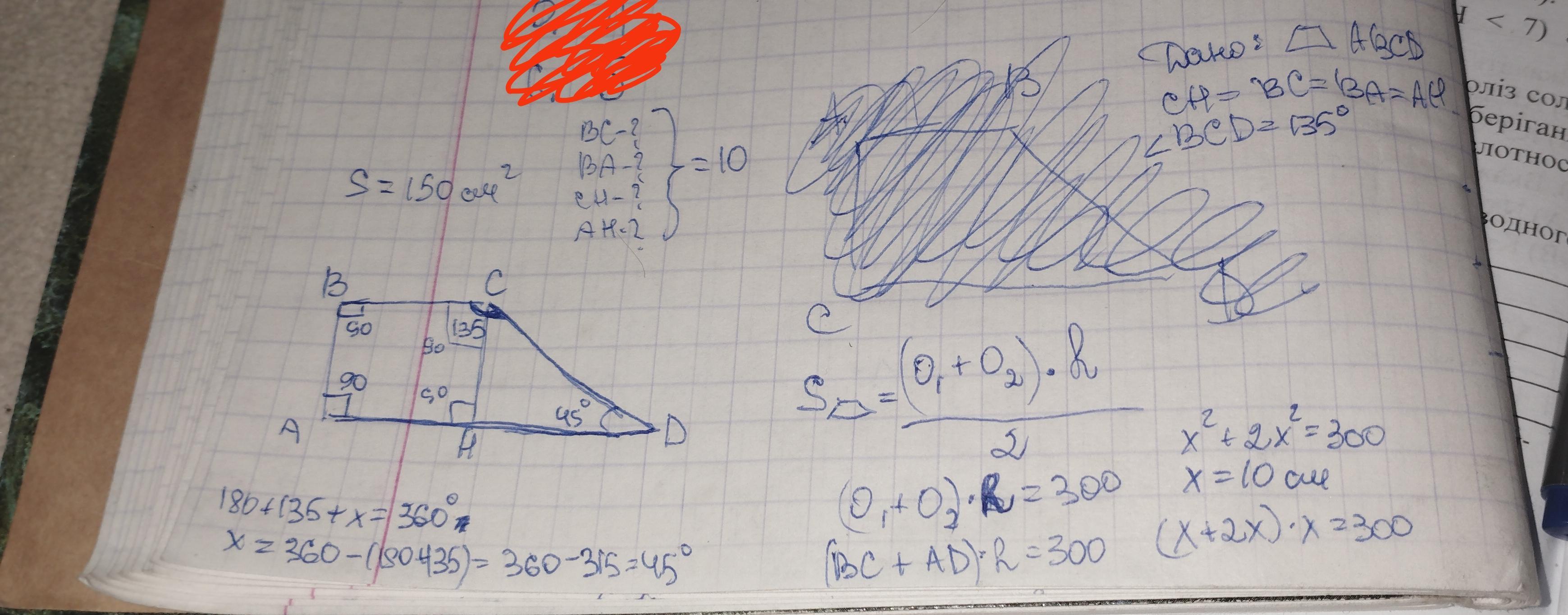
Дана прямоугольная трапеция ABCD с основаниями AD и BC. Площадь этой трапеции равна 150 см2, угол ВCD = 135°. Из вершины C на основание AD опущена высота CH. Известно, что CH = BC. Найдите длину CH.

Дано: трапеція АВСД, СН=ВС=ВА=АН, кут ВСД=135°.

площа трапеції = (основа 1 + основа 2) * на висоту(h) і цей добуток розділити на два. так як нам задана площа з самого початку, то ми можемо підствити. (ВС+АД)*h=300, бо ми перенесли 2, і у нас вийшло 300, бо 150 помножили на 2. через те, що у нас АВСН квадрат, а кут ВСД 135°, то ми можемо зробити висновок, що ВС в два рази менше за АД, а тобто основа 2 = подвоєна основа 1. основу 2 ми можемо записати, як х, а основу 1, як х подвоєне, а тобто 2х. висоту також позначаємо х, бо вона сторона нашого квадрата, а у квадраті всі сторони рівні, тобто СН=ВС. підставляємо ікси замість букв: (х+2х)*х = ЗОО. розкриваємо дужки. виходить х² +2х²= ЗОО. 3х²= З00. х²=100, бо обидві частини рівняння скоротили на три. х=+-10. але це сторона, а сторона не може бути від'ємною, отож, нам підходить тільки додатнє число, тобто 10. Відповідь: СН=10см