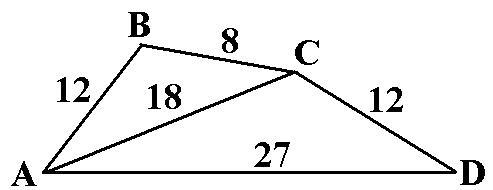
АВСD – довільний чотирикутник, у якого АВ = 12 см, ВС = 8 см, СD = 12 см, АD = 27см. Знайти АВС, якщо АСD = 123°.

Ответ:

Щоб знайти площу чотирикутника ABCD, нам потрібно скористатися законом косинусів. Назвемо кут між AB і CD ACB.

Використовуючи закон косинусів, ми можемо знайти значення ACB:

ACB = cos^-1((AB^2 + CD^2 - AD^2) / (2 * AB * CD))

Підставляючи наведені значення, отримуємо:

ACB = cos^-1((12^2 + 12^2 - 27^2) / (2 * 12 * 12))

ACB = cos^-1(144 / 144) = cos^-1(1) = 0°

Оскільки кут ACB дорівнює 0°, чотирикутник ABCD є паралелограмом, а це означає, що його протилежні сторони паралельні й однакові за довжиною. Отже, AB = CD = 12 см і BC = AD = 27 см.

Нарешті, щоб знайти площу паралелограма ABCD, ми помножимо довжину однієї сторони (AB) на висоту (BC):

Площа ABCD = AB * BC = 12 см * 27 см = 324 квадратних см

Отже, площа чотирикутника ABCD дорівнює 324 см2.

Объяснение: