-
1. Даны вершины треугольника ABC: A(3;-1;0), B(1; 2; 5), С(3;2; -1). Найдите длину Медианы АМ.2. Начало отрезка MN находится в точке М(1;-2; -4). Точка К (-2; 0; 1) делит его пополам. Найдите координаты точки М3. Сфера задача уравнением x2 + y 2 +22+4x2 = 11. Найдите координаты центра и радиус сферы.4. Найдите значение т, при котором точка А(2; m; - 3) принадлежит сфере x+y+z-2y+64x= 22
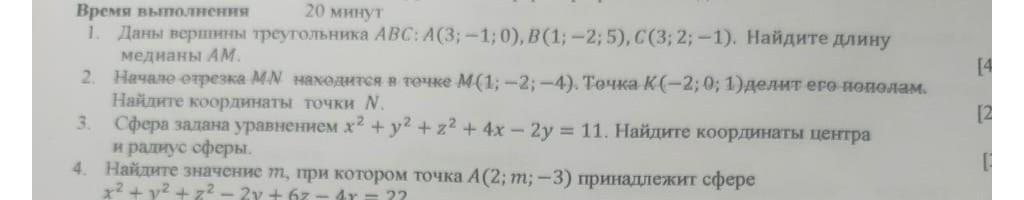
Ответы 1
-
Відповідь:
1.Для начала найдем координаты точки М, которая является серединой стороны BC треугольника ABC. Координаты точки М равны средним арифметическим координат точек B и C:
M = ((1+3)/2; (2+2)/2; (5-1)/2) = (2; 2; 2)
Теперь можем найти длину медианы АМ. Для этого найдем координаты точки М1, которая является серединой стороны AB, и проведем линию М1М. Точка М1 имеет координаты:
M1 = ((1+3)/2; (-1+2)/2; (0+5)/2) = (2; 1/2; 5/2)
Теперь можем найти координаты точки АМ1 и вычислить ее длину:
AM1 = sqrt((2-3)^2 + (2-1/2)^2 + (2-5/2)^2) ≈ 2.72
Таким образом, длина медианы АМ приблизительно равна 2.72.
2.Поскольку точка К делит отрезок MN пополам, координаты точки М являются средними арифметическими координат точек K и N. Значит, координаты точки М равны:
M = ((1-2)/2; (-2+0)/2; (-4+1)/2) = (-1/2; -1; -3/2)
Таким образом, координаты точки М равны (-1/2; -1; -3/2).
3.Уравнение сферы имеет вид x^2 + y^2 + 2^2 + 4x^2 = 11, где координаты центра сферы равны (-2, 0, -2), а радиус равен sqrt(2).
Для этого можно переписать уравнение сферы в каноническом виде:
(x+2)^2 + y^2 + (z+2)^2 = 7
Тогда центр сферы имеет координаты (-2, 0, -2), а радиус равен sqrt(7).
4.Чтобы точка А принадлежала сфере, ее координаты должны удовлетворять уравнению сферы:
x^2 + y^2 + z^2 - 2y + 64x = 22
Подставляем координаты точки А и получаем уравнение относительно t:
2^2 + m^2 + (-3-t)^2 - 2m + 64(2) = 22
Раскрываем скобки и приводим подобные слагаемые:
m^2 - 2m + 4 + t
-
Автор:
cesar711 - 2 года назад
-
8
-
-
Добавить свой ответ
- найдите значение y(0),y(2),y(-3) для функции y=-0,5+2
-
если проехать определенное расстояние на велосипеде со скоростью 24 км/ч, то на его преодоление потребуется на 24 минуты меньше, чем если бы вы ехали со скоростью 20 км/ч, найдите это расстояние
Помогите пожалуйста
-
Предмет:
Математика -
Автор:
spike97 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
ПОМОГИТЕ ПОЖАЛУЙСТА ОЧЕНЬ СРОЧННООООО.
Сочинение по русскому на тему "Книга - наш друг и советчик"
-
Предмет:
Русский язык -
Автор:
bruce51 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Помогите ответить на вопрос по А. Алексин "Домашнее сочинение"
-
Предмет:
Русский язык -
Автор:
bethanyvega - 2 года назад
-
Ответов:
1 -
Смотреть
-
