7. Дан параллелепипед ABCDA,B,C,D1 . B1A1 = ā, BC = bBB = С. Разложите вектор В, М Б,В,В по векторам ã, b, c, если М = [AC] принадлежит [BD]​

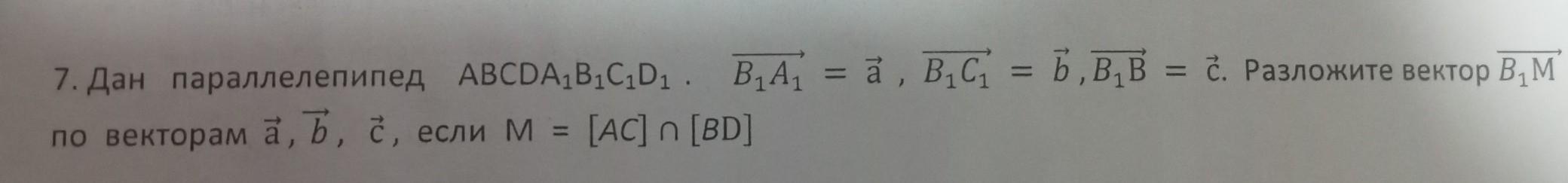
Ответ:

Давайте начнем с определения векторов a, b и c на основе предоставленной информации.

Исходя из приведенной информации, у нас есть:

ABCDA = a + b + c + d + a

B = b

C = b + b

D1B1A1 = d + b + a + b + a

Чтобы разложить вектор B в терминах a, b и c, нам нужно найти скаляры x, y и z такие, что:

B = xa + yb + z*c

Чтобы решить для x, y и z, мы можем использовать тот факт, что M = [AC] принадлежит [BD]. Это означает, что вектор от B до D является скалярным кратным вектору от A до C, или:

D - B = t*(C - A)

где t - скаляр. Мы можем подставить выражения для A, B, C и D, чтобы получить:

(d + b + a + b + a) - b = t*(2b + c - a - b)

Упрощая, мы получаем:

d + a = t*(b + c - a)

Аналогично, мы можем использовать тот факт, что M принадлежит [BD], чтобы получить:

M - B = s*(D - B)

где s - скаляр. Подставляя, как и прежде, мы получаем:

(b + b) - b = s*((d + b + a + b + a) - b)

Упрощая, мы получаем:

b = s*(2a + 2b + d)

Теперь у нас есть два уравнения, включающие a, b и c:

d + a = t*(b + c - a)

b = s*(2a + 2b + d)

Мы можем решить для a и b в терминах c во втором уравнении и подставить в первое уравнение, чтобы получить уравнение, включающее только c:

d + a = t*(3c - a - d)

b = s*(2a + 2s - d) = s*(4c - a - d)

Решая для a и b в терминах c, мы получаем:

a = (3tc + td - d)/(t + 1)

b = (4sc - sa - sd)/(2s - 1)

Теперь мы можем разложить вектор B в терминах a, b и c, используя эти выражения для a и b:

B = xa + yb + zc

= x(3tc + td - d)/(t + 1) + y*(4sc - sa - sd)/(2s - 1) + z*c

где x, y и z - скаляры, для которых нам нужно решить. Для этого мы можем использовать тот факт, что B = b и C = 2b. Мы можем подставить эти выражения в уравнение декомпозиции, чтобы получить:

b = x*(3tc + td - d)/(t + 1) + y*(4sc - sa - sd)/(2s - 1) + zc

2b = x(3tc + td - d)/(t + 1) + y*(4sc - sa - sd)/(2s - 1) + 2z*c

Упрощая, мы получаем:

x*(3tc + td - d)/(t + 1) + y*(4sc - sa - sd)/(2s - 1) + zc = b

x(3tc + td - d)/(t + 1) + y*(4sc - sa - sd)/(2s - 1) + 2z*c = 2b