^^знайдіть площі зафарбованих фігур MNPK квадрат AB = BC = AC = 6^^​

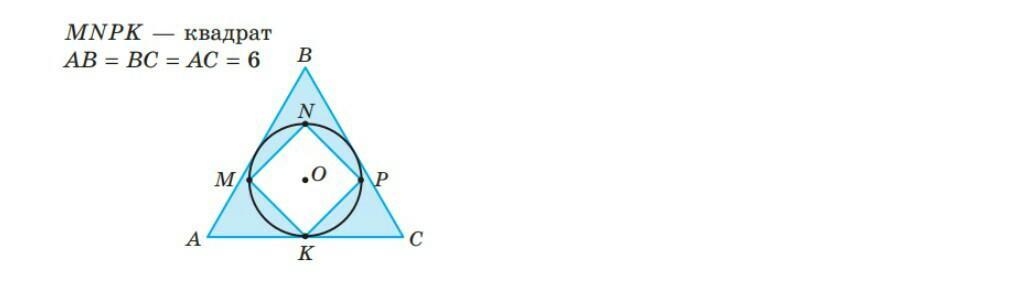
Ответ:

Для знаходження площі зафарбованих фігур потрібно спочатку знайти площу квадрата ABCD:

Площа квадрата ABCD = AB² = 6² = 36 кв. од.

Площа фігури MNPK складається з двох прямокутників та двох трикутників:

Площа прямокутника MNPQ = MN × NP = 3 × 6 = 18 кв. од.

Площа прямокутника KBCP = KB × BC = 3 × 6 = 18 кв. од.

Трикутники MKN та CPK є прямокутними, оскільки вони мають кут 90° в точках K та P відповідно. Тому їхні площі можна знайти за формулою S = 1/2 × a × b, де a та b - довжини катетів.

Площа трикутника MKN = 1/2 × MK × KN = 1/2 × 3 × 3 = 4.5 кв. од.

Площа трикутника CPK = 1/2 × PC × CK = 1/2 × 3 × 3 = 4.5 кв. од.

Отже, площа зафарбованих фігур дорівнює:

Площа фігури MNPK + площа фігури KBCP - площа квадрата ABCD = 18 + 18 - 36 = 0 кв. од.

Отже, площа зафарбованих фігур дорівнює 0 кв. од.