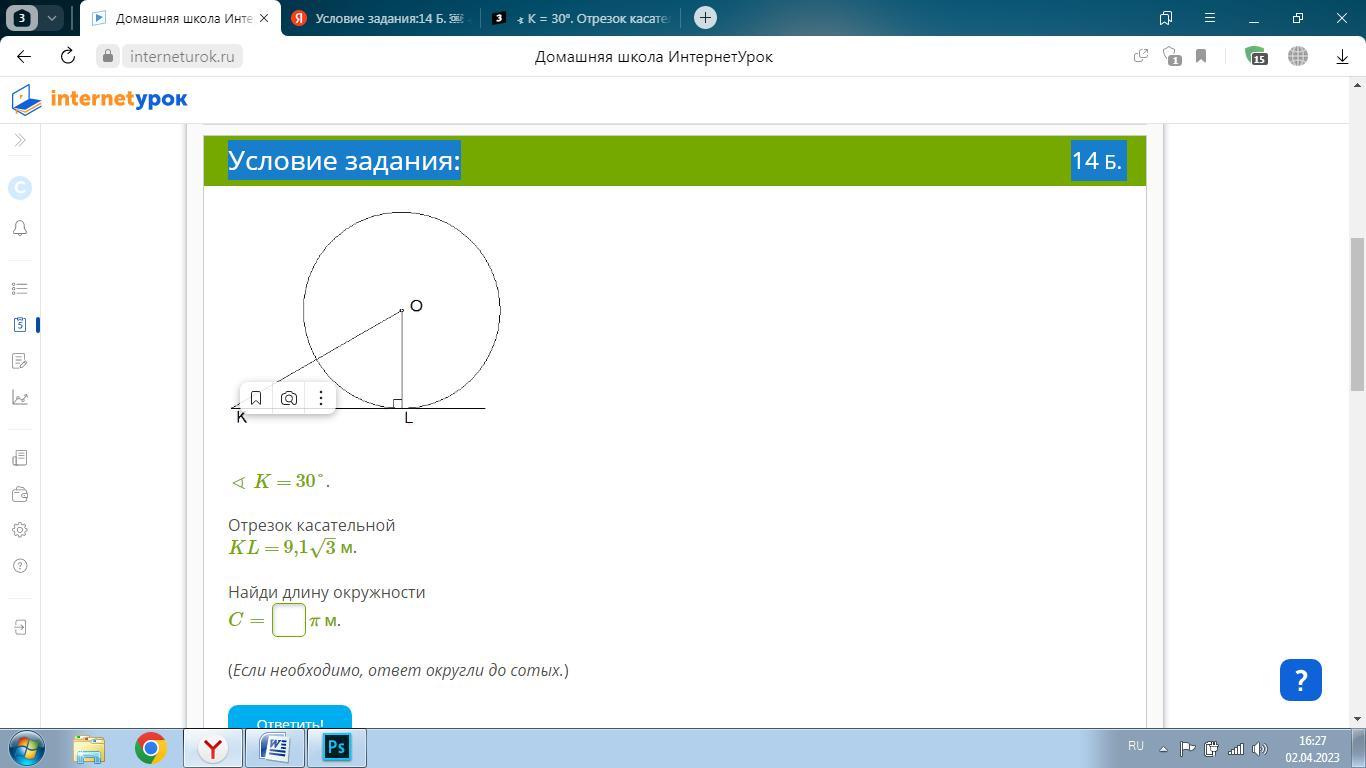
геометрия очень срочно!!!!!!!!!!!!!∢ K = 30°. Отрезок касательной KL = 9,1√3 м. Найди длину окружности C= π м. (Если необходимо, ответ округли до сотых.) Ответить!

Для решения задачи нам нужно знать, что угол между касательной и радиусом окружности, проведенным в точке касания, равен 90 градусов. Также известно, что длина отрезка касательной KL равна 9,1√3 м.

Мы можем использовать теорему Пифагора, чтобы найти длину радиуса окружности. Пусть R - радиус окружности, тогда:

R² = (KL/2)² + KJ²

где KJ - высота, опущенная из центра окружности на отрезок KL.

Так как угол K равен 30 градусов, то угол KJL (образованный касательной и радиусом) равен 60 градусов. Тогда:

KJ = KL/2 * √3 = 4.55 м

Теперь мы можем найти радиус R:

R² = (9.1√3/2)² + 4.55²

R ≈ 6.65 м

Наконец, мы можем найти длину окружности с помощью формулы C = 2πR:

C ≈ 41.74 м (округляем до сотых)

Ответ: 41.74 м.