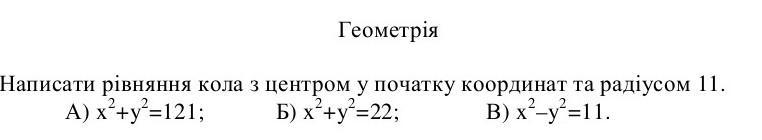Ответы 1
-
Ответ:
Рiвняння кола з центром у початку координат та радiусом 11 мае вид:
x {}^{2} + y {}^{2} = 121
Объяснение:
Напишемо рiвняння кола
(x - a) {}^{2} + (y - b) {}^{2} = r {}^{2} (1)
де а - вiдстань вiд центра кола до початку координат по осi абсцисс
b - вiдстань вiд центра кола до початку координат по осi ординат
r - радiус кола
За умовою задачi центр кола знаходяться у початку координат. Тодi вiдстань вiд центра кола до початку координат по осi абсцисс дорiвнюе нулю, тобто a=0.
Вiдстань вiд центра кола до початку координат.по осi ординат дорiвнюе нулю, тобто b=0
Пiдставимо цi значення у рiвняння (1). Маемо:
(x - a) {}^{2} + (y - b) {}^{2} = r {}^{2}
(x - 0) {}^{2} + (y - 0) {}^{2} = 121
x {}^{2} + y {}^{2} = 121
Отже, рiвняння кола з центром у початку координат та радiусом 11 мае вид:
x {}^{2} + y {}^{2} = 121
Вiдповiдь:
x {}^{2} + y {}^{2} = 121
-
Автор:
otishrod - 2 года назад
-
5
-
-
Добавить свой ответ
-
Найдите наибольшее значение функции у = cos 2x + 3 sin 2x. В ответе укажите квадрат найденного значения.
-
Предмет:
Математика -
Автор:
esperanza12 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
112×12:800 надо выйти 1 каким образом может быть 1
-
Предмет:
Математика -
Автор:
elliott - 2 года назад
-
Ответов:
2 -
Смотреть
-
- Мандрівник проїхав конем деяку відстань за 12 год. За скільки годин автомобіль проїде віддаль у 10 разів більшу, якщо швидкість автомобіля у 4 рази більша від швидкості коня?
-
Отрезки АВ и CD - диаметры окружности с центром О. Найдите периметр треугольника AOD, если известно, что CВ = 15 см, AB = 32 см.
-
Предмет:
Геометрия -
Автор:
gavenproctor - 2 года назад
-
Ответов:
2 -
Смотреть
-