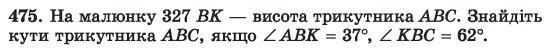Ответы 1
-
Ответ:
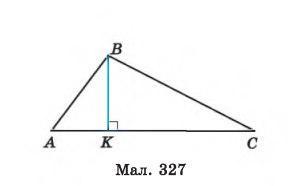
∠ABK + ∠KBC = 37° + 62° = 99°
∠BCK = 180° - 62° - 90° = 28°
Отже, кут BAC (α) дорівнює 53°.
Объяснение:
Для вирішення цієї задачі, ми можемо використати властивості трикутників та геометричні закони.
Позначимо кут BAC як α, кут ABC як β та кут BCA як γ.
З умови, у нас є наступні кути:
∠ABK = 37° (кут між сторонами AB і BK)
∠KBC = 62° (кут між сторонами BK і BC)
Оскільки BK - висота трикутника ABC, ми знаємо, що ∠ABK і ∠KBC є прямими кутами (кути прямокутного трикутника BCK). Тому сума цих двох кутів дорівнює 90°:
∠ABK + ∠KBC = 37° + 62° = 99°
Тепер, щоб знайти кут BAC (α), ми можемо використовувати рівняння суми кутів в трикутнику ABC:
α + β + γ = 180°
Оскільки ми знаємо значення двох кутів, α + γ = 180° - 99° = 81°.
Також, у нас є співвідношення кутів в прямокутному трикутнику BCK:
∠KBC + ∠BCK + ∠BKC = 180°
62° + ∠BCK + 90° = 180°
∠BCK = 180° - 62° - 90° = 28°
Тепер ми можемо знайти кут BAC (α) за допомогою рівняння α + γ = 81°:
α + 28° = 81°
α = 81° - 28°
α = 53°
Отже, кут BAC (α) дорівнює 53°.
-
Автор:
isaiah527 - 2 года назад
-
10
-
-
Добавить свой ответ
-
Розв'яжіть нерівність
(х^2-4)(х^2+х-2)<0
!!!Терміново!!!
-
Предмет:
Математика -
Автор:
willow41 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Заповни таблицю.Vвл. Vт. Vза т. р. Vпроти т. р15 км/год. 3 км/год 13,5 км/год. 10,5 км/год 2 км/год. 11 км/год 21,4 км/год. 20,8
-
Предмет:
Математика -
Автор:
clicker - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Розв'яжіть нерівність:
12+х-х^2>0
Терміново!!!
-
Предмет:
Математика -
Автор:
kristiantrujillo - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
С++
Добавить к коду следующие:
ДВУСВЯЗНЫЙ список
1. Есть указатель на последнюю ячейку (tail).
2. Каждая ячейка знает где находится прошлая.
Код:
#include
#include
using namespace std;
// Одна ячейка односвязного списка
// В структуре всё по-умолчанию public
// T - шаблон. Позволяет создавать объекты, указывая тип данных T
template
struct Node {
T value; // значение ячейки
Node* pNext; // указатель на следующую ячейку
Node(T value = T()) {
this->value = value;
this->pNext = nullptr;
}
};
// Односвязный список
template
class ForwardList {
// Node будет заменяться на Node
typedef Node Node;
Node* head; // указатель на первую ячейку
unsigned int size; // кол-во ячеек (unsigned int - инты без минуса)
public:
ForwardList() {
head = nullptr; // head = 00000000
size = 0;
}
unsigned int GetSize() const {
return size;
}
void PushFront(const T value) {
size++;
// Если список пуст
if (head == nullptr) {
// Создаю новую ячейку и привязываю её к указателю на первую ячейку
head = new Node(value);
// окончить функцию (дальше не сработет)
return;
}
// Если список не был пуст
// Создаю новую ячейку, которая станет первой
Node* temp = new Node(value);
// Следующей от темп будет нынешняя первая ячейка
temp->pNext = head;
// Переключую указатель на первую ячейку на новосозданную
head = temp;
}
void PopFront() {
if (head == nullptr)
return;
// Сохраняем адрес второй ячейки
Node* temp = head->pNext;
// удаляем первую ячейку
delete head;
// переключаем голову на вторую (теперь первую) ячейку
head = temp;
size--;
}
// !!! НЕОПТИМИЗИРОВАННО ИЗ-ЗА СПЕЦИФИКИ ОДНОСВЯЗНОГО СПИСКА
void PushBack(const T value) {
size++;
if (head == nullptr) {
head = new Node(value);
return;
}
// Создаю указатель для перебора ячеек
Node* temp = head;
// Переключаю указатель на последнюю ячейку
while (temp->pNext != nullptr)
temp = temp->pNext;
// Создаю новую ячейку после последней
temp->pNext = new Node(value);
}
// Вывод односвязного списка на экран
void Print() const {
// Создаем указатель для перебора ячеек
// Сначала он будет указывать на первую ячейку
Node* temp = head;
// Перебираем ячейки до тех пор пока не вылезем за пределы
while (temp != nullptr) {
// Вывожу значение ячейки на экран
std::cout << temp->value << " ";
// Переключаю указатель на следующую ячейку
temp = temp->pNext;
}
std::cout << std::endl;
}
bool operator ==(const ForwardList & other) const {
if (this->size != other.size)
return false;
// Указатель для перебора this листа
Node* thisTemp = this->head;
// указатель для перебора other листа
Node* otherTemp = other.head;
// перебираем пока не переберём весь лист
while (thisTemp != nullptr) {
// Если пара ячеек не совпала по значению - списки не равны
if (thisTemp->value != otherTemp->value)
return false;
thisTemp = thisTemp->pNext;
otherTemp = otherTemp->pNext;
}
// Если до сюда ни разу не сработал return false - значит все ок и списки равны
return true;
}
};
int main() {
// DZ
// 1. PopBack (удаление с конца)
// 2. Insert (добавление по индексу)
// 3. RemoveAt (удаление по индексу)
// 4. operator +
// 5. Конструктор копирования
// 6. Сортировка
// 7. GetUnique, который возвращает новый лист ТОЛЬКО из уникальных элементов
ForwardList fl;
fl.PushBack(1);
fl.PushBack(2);
fl.PushBack(3);
ForwardList fl2;
fl2.PushBack(1);
fl2.PushBack(2);
fl2.PushBack(3);
if (fl == fl2)
std::cout << "LISTS ARE EQUAL" << std::endl;
}
-
Предмет:
Информатика -
Автор:
marina64 - 2 года назад
-
Ответов:
1 -
Смотреть
-