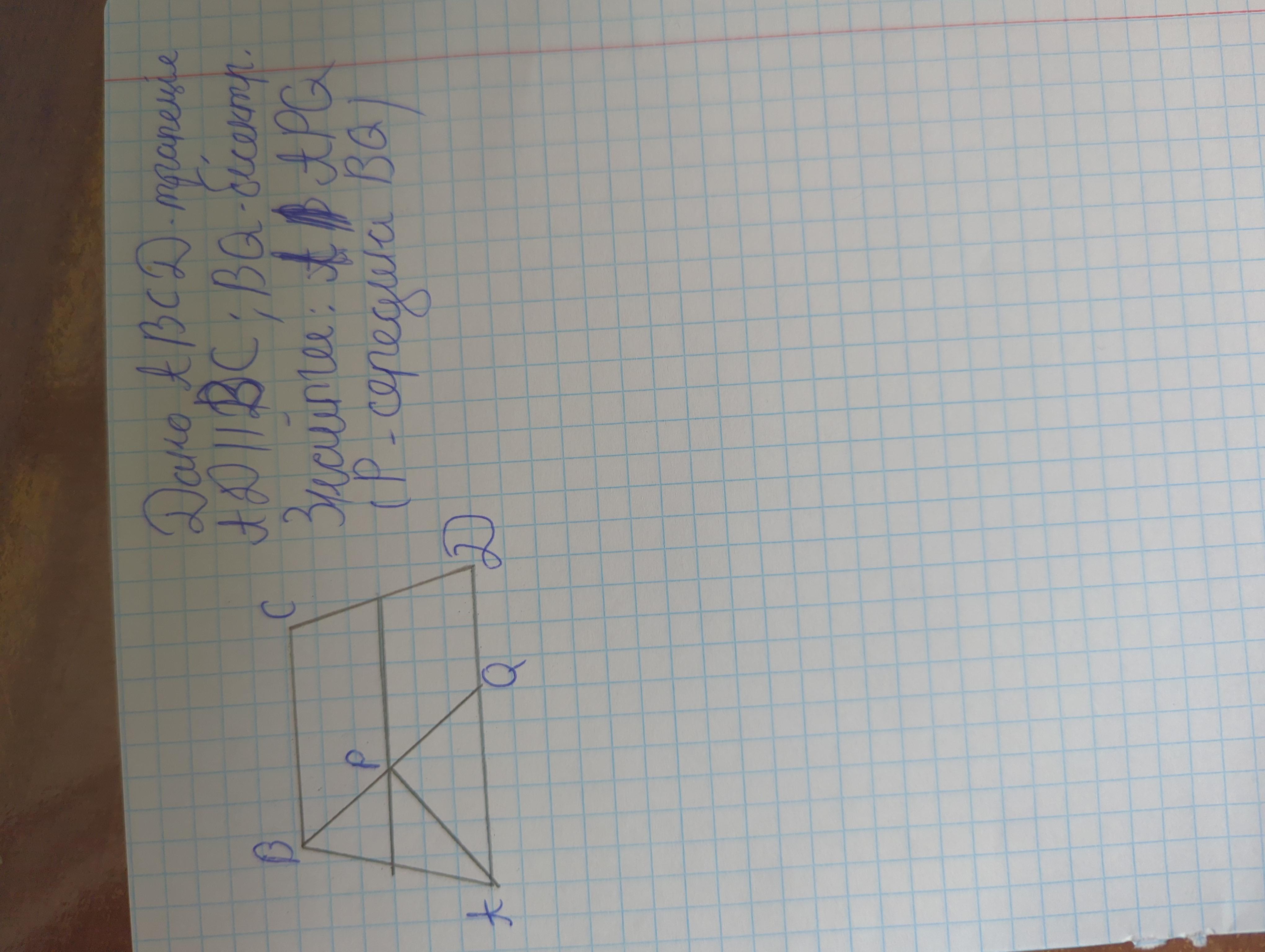
Дано трапецію ABCD AD||BC Відомо що бісектриса кута АBC перетинає середню лінію цієї трапеції в т. Р а основу AD в т. Q знайдіть величину кута APQ (т. P середина BQ)

Відповідь:

Розглянемо трикутник ABC. Оскільки бісектриса кута ABC ділить кут навпіл, то кут ABP дорівнює куту BCQ.

Також, оскільки точка P є серединою відрізка BQ, то кути BPQ і BQP рівні.

Отже, трикутник BPQ є рівнобедреним, а кути BPQ і BQP рівні 60°.

Кут ABP дорівнює куту APQ, а кут ABP дорівнює куту BCQ, отже кут APQ дорівнює куту BCQ, а кут BCQ дорівнює 60°.

Відповідь: кут APQ дорівнює 60°.

Доказ:

ABP = BCQ

BP = BQ

Тому трикутник BPQ є рівнобедреним, а кути BPQ і BQP рівні:

BPQ = BQP = 60°

Також, кут ABP дорівнює куту APQ:

ABP = APQ

Отже, кут APQ дорівнює куту BCQ, а кут BCQ дорівнює 60°:

APQ = BCQ = 60°

Пояснення: