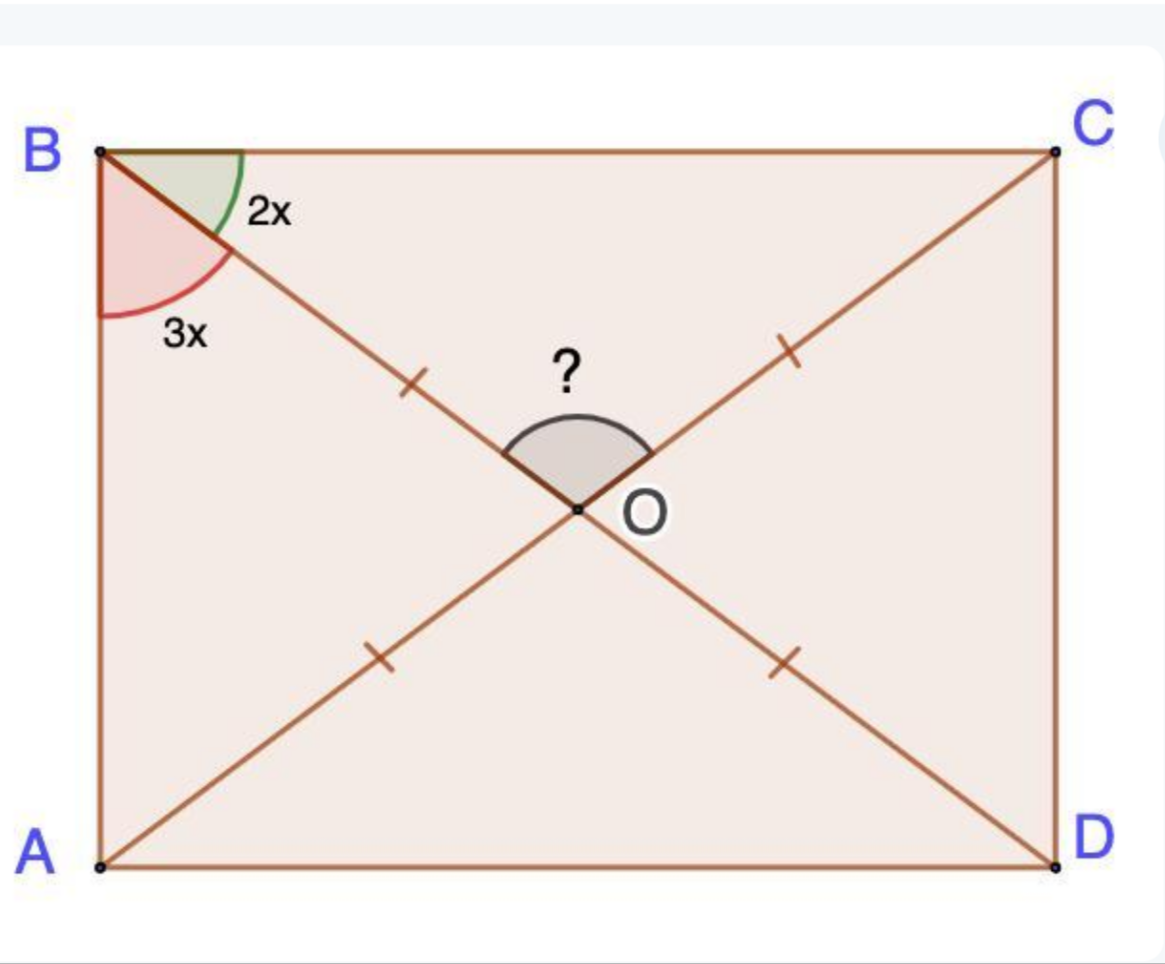
У прямокутнику АВСD точка О – точка перетину діагоналей, Діагональ ділить кут АВС у відношенні 2:3. Знайди більший кут між діагоналями

Ответ:

Больший угол между диагоналями равен 108°.

Объяснение:

В прямоугольнике АВСD точка О - точка пересечения диагоналей, диагональ делит угол АВС в отношении 2: 3. Найди больший угол между диагоналями.

Дано: ABCD - прямоугольник;

AC ∩ BD = O - диагонали;

∠CBD : ∠DBA = 2 : 3

Найти: ∠ВОС

Решение:

∠АВС = 90°

∠CBD : ∠DBA = 2 : 3

Пусть ∠CBD = 2х, тогда ∠DBA = 3х

2х + 3х = 90°

5х = 90° |:5

x = 18°

⇒ ∠CBD = 36°; ∠DBA = 54°

Рассмотрим ΔВОС.

Диагонали прямоугольника равны и точкой пересечения делятся пополам.

⇒ АО = ВО = СО = DО

⇒ ΔВОС - равнобедренный.

Углы при основании равнобедренного треугольника равны.

⇒ ∠CBО = ∠ВСО = 36°

Сумма углов треугольника равна 180°.

⇒ ∠ВОС = 180° - (36° + 36°) = 108°

#SPJ1

Фото в придачу