Мега Мозги ПРОШУ допоможіть Терміново ! 100Б. Розвʼязати з Дано та Малюнком ! Бажано на листочку ,та додати фото !Задача на Фото!

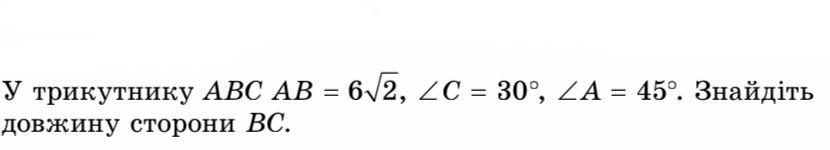
Ответ:

Чтобы найти длину стороны BC в треугольнике ABC, можно воспользоваться законом синусов. Закон синусов гласит, что в любом треугольнике отношение длины стороны к синусу противолежащего ей угла постоянно.

В этом случае мы имеем:

АВ = 6√2

∠LC = 30°

∠LA = 45°

Обозначим длину стороны BC через x. По закону синусов имеем:

грех(LC)/AB = грех(LA)/BC

Подставив значения, получим:

грех(30°) / (6√2) = грех(45°) / х

Теперь мы можем найти х:

x = (sin(45°) * (6√2)) / sin(30°)

Используя тригонометрические значения, расчет упрощается до:

х = (1/√2 * 6√2) / (1/2) = (6 * 2) / (1/2) = 24

Следовательно, длина стороны BC равна 24.

Объяснение: