-
Задача №1.
Высота правильной треугольной пирамиды 12 см, а высота ее основания 15 см. Найдите площадь полной поверхности пирамиды.
Задача №2.
Боковые грани правильной 4-угольной пирамиды наклонены под углом 60⁰ к основанию. Расстояние от середины ребра основания до плоскости противоположной боковой грани равно 4√3. Найдите площадь боковой поверхности пирамиды.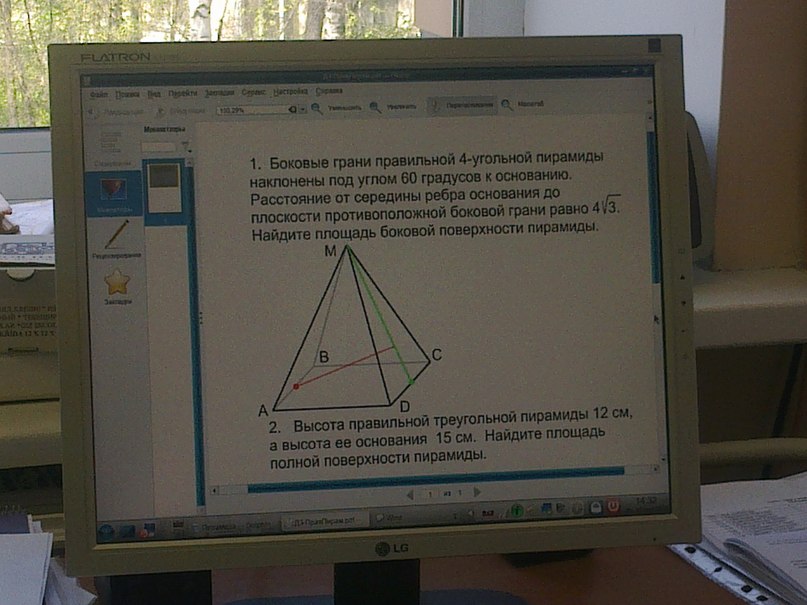
-
Предмет:
Геометрия -
Автор:
santiagoschmidt - 6 лет назад
-
Ответы 1
-
1. (которая на фото - вторая :))
Раз пирамида правильная, то вершина её проектируется на центр основания (центр у правильного треугольника - это точка, где пересекаются все высоты-биссектрисы-медианы-медиатрисы), который лежит на расстоянии 1/3 от высоты основания от стороны основания. Ну, проще говоря, высота 15, а от центра, то есть от точки, куда приходит высота пирамиды, до стороны основания 5.
Таким образом, мы можем рассмотреть прямоугольный треугольник, образованный высотой пирамиды, апофемой (высотой боковой грани) и её проекцией на основание, которая как раз и есть расстояние от центра основания до стороны.
У этого треугольника катеты 5 и 12, поэтому гипотенуза 13 (есть такая Пифагорова тройка 5,12,13; 5^2 + 12^2 = 13^2), а это и есть апофема.
Сторона основания равна 15/(корень(3)/2) = 10*корень(3).
Площадь основания 15*10*корень(3)/2 = 50*корень(3), периметр основания 30*корень(3), плщадь боковой поверхности 30*корень(3)*13/2 = 195*корень(3);
Площадь полной поверхности 245*корень(3);
2. (которая на фото первая)
Тут еще проще. Если соединить отмеченную (но не обозначенную) на рисунке красную точку - пусть это точка К с зеленой точкой - пусть это точка Р, и обе соединить с точкой М, то треугольник КРМ - равносторонний. Ну, то, что он равнобедренный, ясно - МК и МР - это апофемы одинаковых граней, они равны. А поскольку угол МРК задан в задаче, он равен 60 градусов, то есть МКР равносторонний треугольник.
(Отступление. Это и есть линейный угол двугранного угла между боковой гранью и основанием, потому что плоскость МКР перпендикулярна CD. Это надо уметь доказывать! даже если это видно "и так". Дело в том ,что в основании лежит квадрат, поэтому "средняя линяя" КР перпендикулярна CD, и кроме того CD перпендикулярна высоте пирамиды, которая принадлежит проскости МРК. А принадлежит она плоскости МРК, потому что основание высоты пирамиды - это центр квадрата, а он лежит на КР. Раз две точки принадлежат плоскости - вся прямая принадлежит плоскости. Но высота пирамиды перпендикулярна всей плоскости основания, то есть любой прямой в нем, в том числе и CD. Раз СD перпендикулярно двум прямым в MKP, СD перпендикулярно всей плоскости МКР. Поэтому угол МРК - линейный угол двугранного угла. Всю эту "литературу" обычно опускают при решении, или записывают очень кратко. Но надо уметь всё это доказывать, это на много важнее всяких вычислений.)
Итак, заданный отрезок 4*корень(3) - это высота в правильном треугольнике МКР. Поэтому, во-первых, высота пирамиды (это - тоже высота в этом треугольнике, проведенная к другой стороне) равна 4*корень(3). Но это нам не очень надо, а вот что нам надо - это сторона этого треугольника, которая равна 4*корень(3)/(корень(3)/2) = 8.
Итак, в основании пирамиды лежит квадрат со сторонй 8, а четыре боковые грани - равнобедренные треугольники с апофемой 8.
Площадь боковой поверхности 4*8*8/2 = 128. Это ответ.
Надо отметить, что площадь основания 8*8 = 64.
Тут видно, что Sboc*cos(60) = Socn
-
Автор:
cyrusgsk9 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
сколько литров углекислого газа образуется при полном сгорании 0,2 моль ацетилена (н.у)?
-
доказать, что параллелограмм, у которого все углы равны, а диагонали перпендикулярны, вляется квадратом.
-
какие из утверждений верны? 1)через точку,не лежащую на данной прямой,можно провести перпендикулярную прямую к этой прямой 2)треугольник со сторонами 1,2,4 не существует 2)сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон
-
Предмет:
Математика -
Автор:
bandit8 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
на восстановление 5.6 г оксида металла (2) потребовалось 0.14 г водорода. Определите металл, входящий в состав оксида
