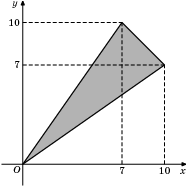
Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10).

Прекрасный чертеж. Надо только продлить "крайние" прямые x = 10 и y = 10 до пересечения в точке (10,10), чтобы получился квадрат. Затемненная фигура - это часть квадрата, а остальные части - это два прямоугольных треугольника с катетами 7 и 10 и еще один треугольник (тот, который получился при продолжении прямых x = 10 и y = 10, "недостающая" половинка квадрата 3х3) - равнобедренный прямоугольный с катетами 3.

Поэтому площадь темной фигуры

S = 10^2 - 2*(7*10/2) - 3^2/2 = 100 - 70 - 9/2 = 25,5.

Обозначим вершины тр-ка О(0; 0), А(7; 10), В(10;7).

Найдём длины сторон: ОА = √((7-0)² + (10-0)²) = √149

                                    ОВ = √((10-0)² + (7-0)²) = √149

Треугольник ОАВ - равнобедренный (ОА = ОВ)

                                    АВ = √((10-7)² + (7-10)²) = √18

Середина С отрезка АВ имеет координаты

                                    хС = (7+10)/2 = 8,5

                                    уС = (10+7)/2 = 8,5

Высота ОС тр-ка ОАВ равна

                                    ОС = √((8,5-0)² + (8,5-0)²) = √144,5

Плищадь тр-ка ОАС равна

S = 0.5·AB·OC = 0.5· √(18·144,5) = 0.5· √(18·144,5) = 0.5√2601 = 0.5·51 = 25.5

Ответ: S = 25,5