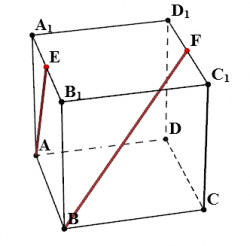
В кубе А...D1 точки Е,F-середины ребер соответственно A1B1 и C1D1.Найдите косинус угла между прямыми AE и BF.

Надо провести из точки F прямую II AE. Ясно, что это FD. Угол между FD и BF, то есть угол BFD и надо найти. Для этого надо найти все стороны треугольника ВFD.

Пусть ребро куба равно 1.

Тогда

ВD = √2;

Ясно, что FD = АЕ = √(1^2 + (1/2)^2) = √5/2;

Отсюда BF = √(ВВ1^2 + B1F^2) = 3/2;

Таким образом, у треугольника BFD стороны FD = √5/2; BF = 3/2; BD = √2;

По теореме косинусов для треугольника BFD получается

BD^2 = FD^2 + BF^2 - 2*BF*FD*x; x = cos(угол BFD);

x = √5/5;