Задать вопрос Регистрация
Помочь другим

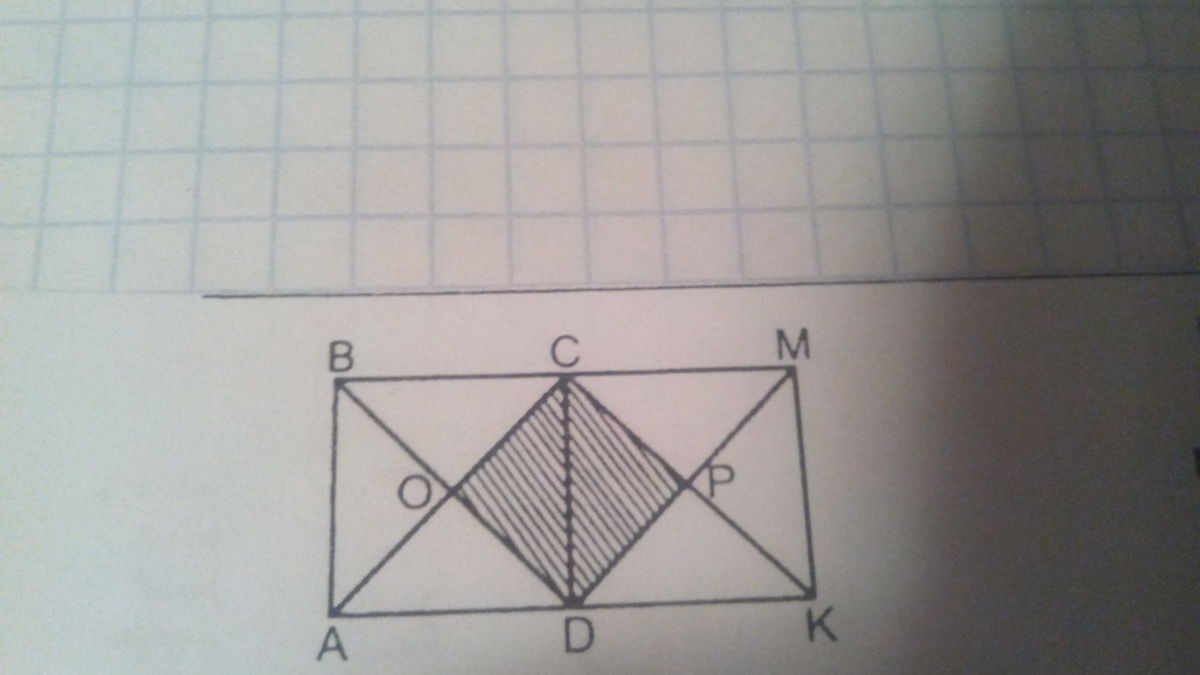
  • ABCD и DCMK - квадрат AB = 6 см. Найдите площадь и периметр четырехугольника OCPD

    question img

Ответы 2

  • Ответ: площадь четырехугольника OCPD равна 18 см², а периметр - 12\sqrt{2} см.

    Решение:

    • Заметим, что OCPD - это квадрат. Большие квадраты ABCD и DCMK между собой равны, так как имеют общую сторону. Диагонали этих квадратов взаимно перпендикулярны (образуют угол 90°) и точкой пересечения делятся пополам. Все стороны четырехугольника OCPD равны половине диагонали большого квадрата, и, поэтому, также равны между собой. А четырехугольник с углами по 90° и равными сторонами является квадратом.

    Вначале попробуем найти сторону квадрата OCPD. Как было написано выше, каждая его сторона равна половине диагонали больших квадратов. Сама диагональ равна (по теореме Пифагора):

    \displaystyle BD=\sqrt{BA^2+AD^2} =\sqrt{6^2+6^2} = \sqrt{72} = \sqrt{36}\sqrt{2} = 6\sqrt{2}.

    Тогда сторона искомого квадрата равна:

    \displaystyle \frac{6\sqrt{2} }{2} = 3\sqrt{2}.

    Теперь можно найти периметр и площадь:

    \displaystyle P_\square = 4a =4*3\sqrt{2} = 12\sqrt{2}\; cm.\\\\S_\square = a^2 =(3\sqrt{2})^2 =3^2\sqrt{2} ^2 =9*2=18\; cm^2.      

  • Ответ:

    Объяснение:

    OCPD - квадрат со стороной, равной половине диагонали квадрата ABCD, при стороне АВ = 6 см.

    Квадраты ABCD и DCMK одинаковы, и они имеют общую сторону. Диагонали этих квадратов взаимно перпендикулярны и точкой пересечения делятся пополам. Все стороны OCPD равны половине диагонали большого квадрата, и, поэтому, также равны между собой. А четырехугольник с прямыми углами и равными сторонами является квадратом.

    AC = BD = 6√2 см.

    OC = CP = PD = OD = AC/2 = 3√2 см.

    Периметр P = 4*3√2 = 12√2 см.

    Площадь S = (3√2)^2 = 9*2 = 18 кв.см.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years