Задать вопрос Регистрация
Помочь другим

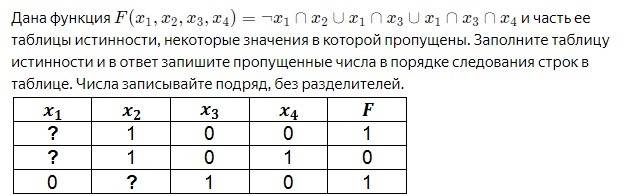
  • Задача с таблицей истинности, ответ 011, мне нужно только подробное решение!

    question img

Ответы 2

  • Берем и подставляем.

    F = 1 \Rightarrow \\ 1 = \lnot x1 \cap 1 \cup x1 \cap 0 \cup x1 \cap 0 \cup 0 \\ X \cap 1 = X \\X \cap 0 = 0 \Rightarrow \\1 = \lnot x1 \cup 0\cup 0 \cup 0 \\ \cup = or \Rightarrow \\ 1 = \lnot x1 \cup 0 \\ x1 = 0 \Rightarrow \lnot x1 = 1 \Rightarrow \\ 1 = 1\cup 0 \Rightarrow 1 = 1

    И так далее Подставляем, сокращаем и получаем то что нужно. Знать надо обычные правила преобразования логических выражений.

    Во второй строке получаем все тоже самое, но F = 0 . Больше там ничего не меняется, следовательно x1 = 1

    F = 1 \Rightarrow \\ 1 = 1 \cap x2 \cup 0 \cap 0 \cup 0 \cap 0 \cup 0 \\ X \cap 1 = X \\X \cap 0 = 0 \Rightarrow \\1 = x2 \cup 0\cup 0 \cup 0 \\ \cup = or \Rightarrow \\ 1 = x2 \cup 0 \\ x2 = 1 \Rightarrow 1 = 1

    • Автор:

      oswaldo42
    • 6 лет назад
    • 0

  • Для начала попытаемся функцию упростить.

    \lnot x_1\land x_2\lor x_1 \land x_3\lor x_1\land x_3\land x_4=\overline{x_1}x_2+x_1x_3+x_1x_3x_4=\\ \overline{x_1}x_2+x_1x_3(1+x_4)=\overline{x_1}x_2+x_1x_3

    x₄ ушло, жить стало легче.

    А теперь берем каждую строку подставляем известные значения.

    Для первой строки

    F=\overline{x_1}x_2+x_1x_3 \\ 1=\overline{x_1}\cdot 1+x_1\cdot0\\ 1=\overline{x_1} \to x_1=0

    Для второй строки

    F=\overline{x_1}x_2+x_1x_3 \\ 0=\overline{x_1}\cdot 1+x_1\cdot0\\ 0=\overline{x_1} \to x_1=1

    И для третьей строки

    F=\overline{x_1}x_2+x_1x_3 \\ 1=1\cdot x_2+0\cdot1 \\ 1=x_2

    Ответ действительно 011.

    • Автор:

      mckenna
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years