-
Найдите наибольшее и наименьшее значения функции на заданном отрезке:
y=1/2x^4-9x^2 , [-1;4]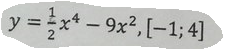
-
Предмет:
Математика -
Автор:
damarijx4r - 6 лет назад
-
Ответы 1
-
Находим экстремумы функции 0,5х⁴ - 9х².Для этого определяем производную заданной функции:f' = 2x³ - 18x.Приравниваем её нулю:2x³ - 18x = 02x(x² - 9) = 0x₁ = 0x² - 9 = 0x² = 9x₂ = 3x₃ = -3 - это значение не входит в заданный предел и его отбрасываем.Теперь определим, где минимум, а где максимум.Для этого наблюдаем, как ведёт себя производная вблизи точек экстремума.Примем х = 1 f' = 2*1³-18*1 = -16 - значение отрицательно.Примем х = -1 f' = 2*(-1³)-18*(-1) = 16 - значение положительно.Значит, 0 - это точка максимума.Значение функции равно f = 0.Аналогично рассматриваем точку х = 3.Здесь будет минимум функции на заданном пределе:f = 0.5*3⁴ - 9*3² = 81/2 - 81 = -40.5.
-
Автор:
ahmad - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите.Надо написать доклад на тему:дикие животные по природоведению.
-
Предмет:
Биология -
Автор:
gianaoneill - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите по географии. 7 класс. Пожалуйста.
Используя данные таблицы "Крупнейшие реки Евразии по длине", диаграммы "Крупнейшие реки Евразии по площади водосборного бассейна" и карты "Внутренние воды Евразии", определите названия пяти рек, являющихся крупнейшими по совокупности показателей: длине, площади бассейна и годовому стоку. Выпишите значения показателя объёма годового стока для этих рек. -
Помогите ПЛИЗ...
как будет "Go" в будущем времени.
как будет "Are" в прошедшем времени.-
Предмет:
Английский язык -
Автор:
fresier - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Укажите конструкции,которые не являются словосочетаниями:
1. в течение полугодия
2. выполнили качественно
3.разноцветные шарики
4.сады великолепны
5. спелые и сочные
-
Предмет:
Русский язык -
Автор:
simon942 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
