-
Найдите наименьшее значение функции y=(3x^2-36x+36)e^(x-10) на отрезке [8;11]
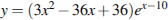
-
Предмет:
Математика -
Автор:
mochag73t - 6 лет назад
-
Ответы 4
-
Че это вдруг?
-
Автор:
mariahharrell - 6 лет назад
-
0
-
-
Я там ошиблась при вычислении, а исправлять было некогда, убегала по делам. Могу сейчас правильное решение написать :)
-
Автор:
margaretdaniels - 6 лет назад
-
0
-
-
Увы, исправить решение уже не могу, а в комментариях формулы не вставляются. Попробую так написать.y'(x)=(6x-36)*e^(x-10)+(3x^2-36x+36)*e^(x-10)y'=0 => e^(x-10) *(6x-36+3x^2-36x+36)=0, e^(x-10)>0 =>3x^2-30x=0x^2-10x=0x(x-10)=0x1=0 не принадлежит [8;11], x2=10 - точка экстремума. Подставляем в функцию:y(8)=(3*8^2-36*8+36)*e^(8-10)=-60e^(-2)=-60/(e^2)=-60/(2,7^2)=-8,23y(10)=(3*10^2-36*10+36)*e^(10-10)=-24y(11)=(3*11^2-36*11+36)*e^(11-10)=3e=8,1.Наименьшее значение y(10)=-24
-
Автор:
jessie74 - 6 лет назад
-
0
-
-
Удалите, пожалуйста!
-
Автор:
preciousvalentine - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите)))) кроме решение нужно еще и правильное оформление) заранее, спасибо) При згорянні органічної речовини масою 2,3 г в надлишку кисню утворився карбон діоксид масою 4,4 г і вода масою 2,7 г. Відносна густина випарів цієї речовини за воднем дорівнює 23. З яких елементів складається речовина? Визначити її формулу
-
Предмет:
Химия -
Автор:
shakirat0va - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
1. Найдите вид связи в словосочетании - управление:
а) встретить вас; г) вдохновенно трудиться;
б) поворот налево; д) в туристском походе;
в) учить уроки; е) постоянные заботы.
2. Укажите повествовательное предложение.
А. Люблю тебя, Петра творенье!
Б. А вы любили когда-нибудь?
В. Любите нас, хороших, добрых, милых.
Г. Любовь моя, приди ко мне, приди!
3. Найдите предложение, в котором подлежащее выражено при-частием.
А. Отъезжающие вошли в вагон.
Б. Бывалые и старые поучали молодых.
В. Несколько провожающих стояли у вагона.
Г. Встречающие, пройдите на второй путь.
4. Укажите предложение с составным глагольным сказуемым.
А. Он казался очень смелым.
Б. Я буду решать задачи.
В. Жить — Родине служить.
Г. Ты обязан хорошо учиться.
5. Найдите пример с выделенным словом — прямым дополне¬нием.
А. Конек режет лед.
Б. Встретить ночь готовится природа.
В. Осень сменяет лето.
Г. Отпуск мы провели очень весело на Черном море.
6. Укажите предложение с несогласованным определением.
А. Желание наказать дерзкого обидчика было очень сильно.
Б. Новогодняя елка была украшена необыкновен¬но красиво.
В. Еще не ставший знойным воздух приятно ос¬вежает грудь.
Г. Сбылась мечта увидеть Москву.
7. Найдите предложение, в котором определение выражено име¬нем существительным.
А. Деревенские улицы просто тонули в густой зелени.
Б. На чернобровом парне была ярко-красная ру¬баха навыпуск.
В. Лестница на чердак была очень крутая.
Г. Книга оказалась в портфеле.
-
Предмет:
Русский язык -
Автор:
solomonb7ax - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите с немецким Setzen Sie das passende Reflexivpronomen ein :
1. Setzt ...!
2. Wir sollen ... wärmer anziehen.
3. Ich muss ... von Ihnen verabschieden.
4. Mit wem hast du ... unterhalten ?-
Предмет:
Другие предметы -
Автор:
bennyld4q - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
1)arc sin0+ arc cos0+ arc tq0
2)sinx +sin2x- cosx-2cos( степень 2)x
3)tq3x * cos(степень 2)х - tq3x * sin(степень 2)х
-
Предмет:
Алгебра -
Автор:
connorkaca - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
