-
(39)Приложения определенного интеграла. Длина дуги кривой\ Решить как можно подробнее
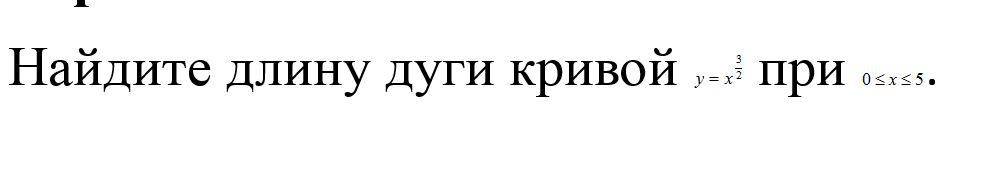
-
Предмет:
Математика -
Автор:
rosalia3e5c - 6 лет назад
-
Ответы 1
-

-
Автор:
marianaknight - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Служебные части речи:
А) называют действия
В) выражают отношения между словами
С) Указывают на предметы
Д) Называют признаки предметов
Е) Называют качества предметов
-
Предмет:
Русский язык -
Автор:
jared29 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Молю!!! Очень надо!!!! Помоги!!! Срочно!!!
Водитель машрутки знает: чтобы успеть доехать из А в В, не отстав от расписания, он должен ехать без остановок со скоростью 50 км/ч. Но поскольку на первой половине пути он попал в пробку, ему пришлось ехать со скоростью 25 км/ч. Однако на второй половине пути движение было свободное, и ему удалось проехать её со скоростью 100 км/ч. Успел ли он вовремя? -
Герои рассказа Шолохов"Они сражались за Родину"
-
Предмет:
Литература -
Автор:
adelawilson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите решить задачу зарание спасибо
В рулоне 50 м ткани. От него отрезали кусок на 4 костюма по 3 метра в каждом.Сколько метров ткани осталось-
Предмет:
Математика -
Автор:
miley - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
