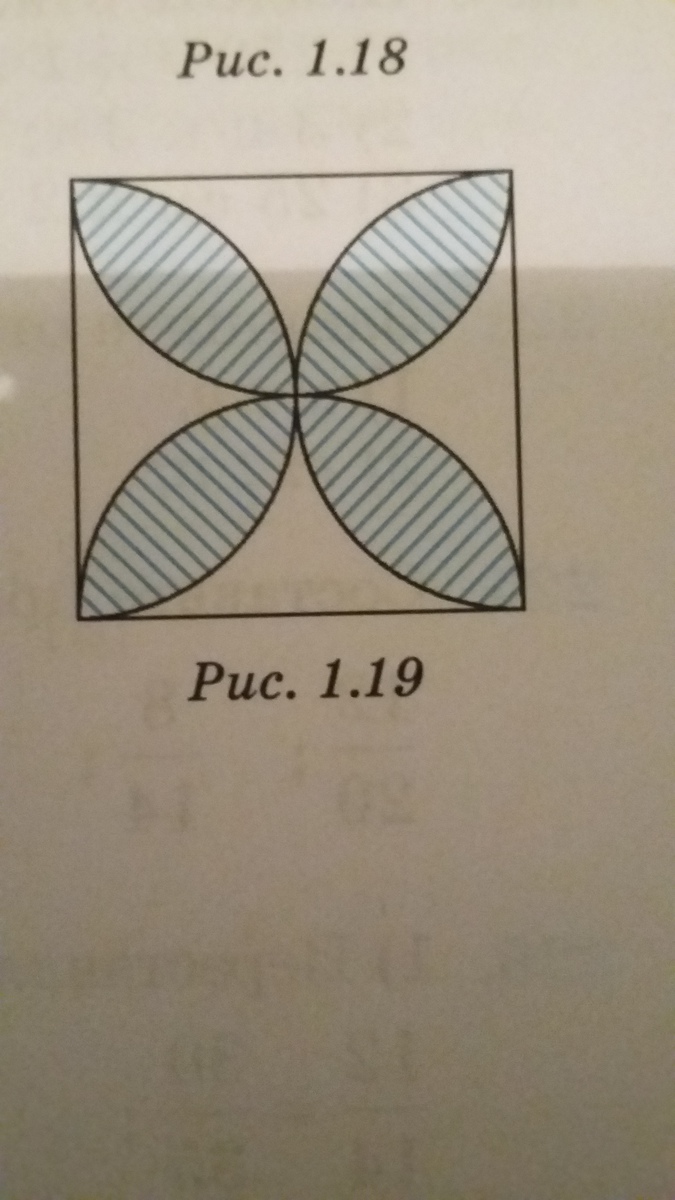
на рисунке 1. 19 изображен квадрат со стороной 20 см. найдите площадь закрашенной части квадрата

Из рисунка задания видно, что искомая фигура образована четырьмя полукругами, построенными на сторонах (обозначим их D) квадрата, являющимися также  диаметрами этих полукругов. Оставшиеся части (Sс) квадрата, не занятые фигурой , обозначим 1,2,3, 4. (См.приложение). На рисунке видно, что сумма площадей противоположных свободных частей (1и3) равны разности площадей квадрата и 2-х полукругов, построенных на перпендикулярных сторонах(2и4). Также и сумма площадей свободных частей 2 и 4 равна разности площади квадрата и двух других полукругов (1и3). Площадь квадрата Sк=20·20=400 (см²) . Сумма площадей двух полукругов равна площади круга Sо=πD²/4 = 3,14·400/4=314 (см²). Тогда сумма площадей двух свободных частей равна: 400-314=86 (см²), а всех четырех (S)свободных частей: S=86·2=172 (см2).Площадь же искомой фигуры равна разности площади квадрата и площади  свободных частей. т.е. Sф=Sк-S=400-172=228(см²). Ответ: Площадь фигуры в данной задаче равна 228см²В приложении дано решение в общем виде с выводом формулы для вычисления данной фигуры. (То, что она образована именно полукругами, объясняется  тем, что мы имеем дело с квадратом.).