-
Помогите с алгеброй умоляю срочно!!! 45 баловв!!
нужно решение!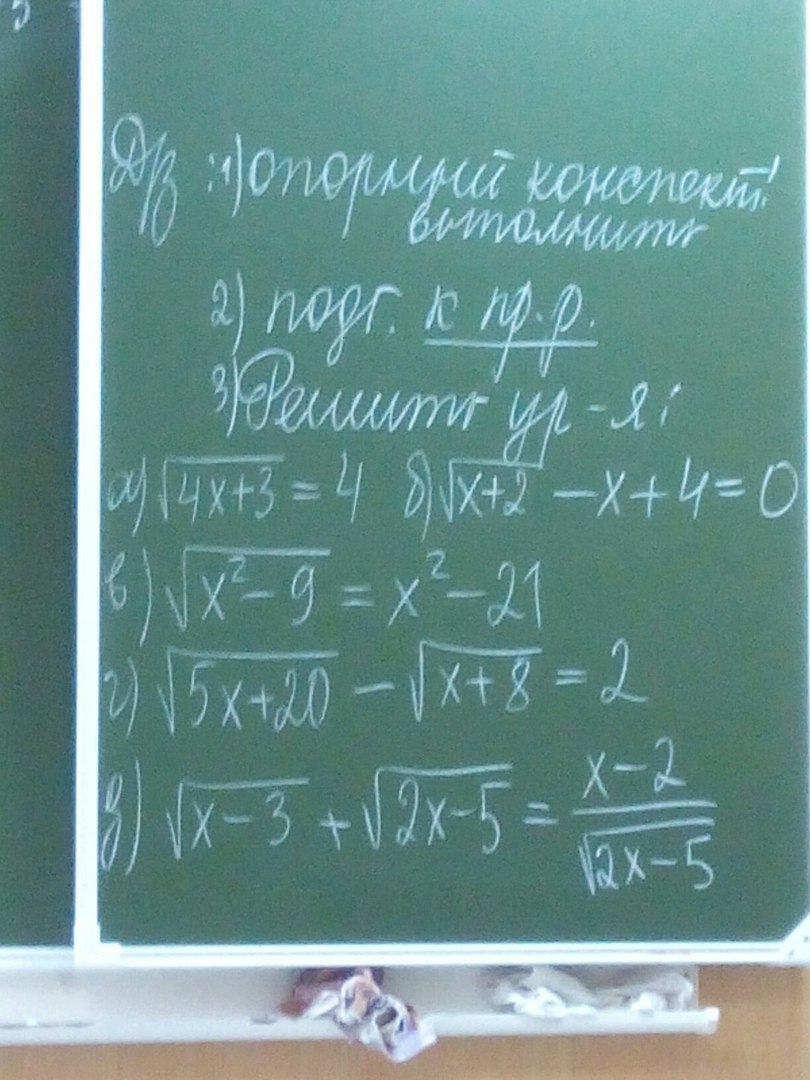
-
Предмет:
Математика -
Автор:
craigabbott - 6 лет назад
-
Ответы 1
-
а)√(4х+3)=4ОДЗ 4х+3>=0 => х>=-0.75 возведем в квадрат лева и право4х+3=164х=13х=13/4=3.25б) √(х+2)=х-4ОДЗ х+2>=0 х>=-2возведем в квадратх+2=(х-4)^2х^2-8х+16-х-2=0х^2-9х+14=0Д=81-56=25х1=(9-5)/2=2х2=(9+5)/2=7в)√(х^2-9)=х^2-21одз х^2-9>=0 (х-3)(х+3) >=0 + - +______-3_________3_______х принадлежит от (-бесконеч ; -3] U [3 ; + бесконеч]заменим √( х^2-9)=tt>=0t=t^2-12t^2-t-12=0D=1+48=49t1=(1-7)/2=-3 не подходит t>0t2=(1+7)/2=4√(х^2-9)=4х^2-9=16х^2=25х1=5х2=-5г)√(5х+20)=2+√(х+8)ОДЗ 5х+20>=0 => х>=-4ОДЗ х+8>=0 =>х>=-8 х>-4√(5х+20)=25х+20=4+4√(х+8)+х+84х+8=4√(х+8)х+2=√(х+8)ОДЗ х+2>=0х>=-2х^2+4х+4=х+8х^2+3х-4=0Д=9+16=25х1=(-3-5)/2=-4 не подходитх2=(-3+5)/2=1д)домножим на √(2х-5) ОДЗ х-3>=0 х>=32х-5>0 х>2.5отсюда х>=3√(х-3)*√(2х-5)+2х-5=х-2√(2х^2-6х-5х+15)=-х+3ОДЗ -х+3>=0-х>=-3х<=3 но по первому ОДЗ х>=3тогда единственное значение х удовлетваряющее этим областям допустимых значений является корень х=3ответ х=3
-
Автор:
alfieuesm - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Спортсмен массой 70 кг готовится к выполнению прыжка с трамплина. Чему равна сила тяжести, действующая на спортсмена, и вес спортсмена? Чему равны эти силы во время прыжка?
-
Может ли сумма каких-то 2015 последовательных натуральных чисел быть равна сумме каких-то 2016 последовательных натуральных чисел?
подробно-
Предмет:
Математика -
Автор:
kit-kat - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите нарисовать план дома и написать пять предложений на английском
-
Предмет:
Английский язык -
Автор:
bradley100 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- Какой обєм мает 100 молей ртути?
How much to ban the user?
1 hour
1 day
100 years
