-
Вычислить интеграл, выделив целую часть дроби (применяя деление «уголком» многочлена на многочлен) и разложив интеграл на сумму более простых интегралов.
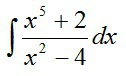
-
Предмет:
Математика -
Автор:
priscilawmp8 - 5 лет назад
-
Ответы 1
-
_ x⁵ + 2 | x²-4 x⁵- 4x³ x³+4x --------- _ 4x³+2 4x³-16x --------- 16x +2 (x⁵+2)/(x²-4)=x³+4x + (16x+2/(x²-4))
-
Автор:
merclekoch - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
составь слова на чу щу
-
Предмет:
Русский язык -
Автор:
rolandowyatt - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Выполните деление :
1) 15,3 : (- 1,7)
2) -20,7 : (- 9)
3) - 7/17 (/ - это дробь) : (- 49/34)
4) Одна целая 2/9 : (- семь целых 1/3)
5) - 5,6 : одну целую 2/5
6) -4.9 ^ (- 1,6)
7) 0,1 : (- 1/12)
8) - 0/18 : одну целую 4,5.
! ! ! ! ! ! ! ! ! ! ! ОБЯЗАТЕЛЬНО С РЕШЕНИЕМ ! ! ! ! ! ! ! ! ! ! !
! ! ! ДАЮ 35 БАЛОВ ! ! !-
Предмет:
Математика -
Автор:
twiggydscf - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
грибы- это животные или растение?
-
Предмет:
Биология -
Автор:
phoebemccarthy - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Вычислить определённый интеграл с точностью до второго знака после запятой.
-
Предмет:
Математика -
Автор:
nathanlopez - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
