Задать вопрос Регистрация
Помочь другим

  • Вычислить определённый интеграл с точностью до второго знака после запятой.

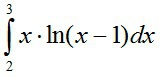
    question img

Ответы 1

  • Вводим замену переменной u=x-1тогда х=u+1, а du=dxПолучили интеграл \int\limits^3_2 {(u+1)ln(u)} \, du= \int\limits^3_2 {(uln(u)+ln(u))} \, du Сначала найдём неопределённый интеграл \int\limits {uln(u)} \, du+ \int\limits {lnu} \, du= u^2( \frac{ln(u)}{2}- \frac{1}{2^2})+(uln(u)-u)= = \frac{u^2ln(u)}{2}- \frac{u^2}{4}+uln(u)-u=uln(u)( \frac{u}{2}+1)-u( \frac{u}{4}+1)+CВводим обратную замену(x-1)*ln(x-1)*( \frac{x-1}{2}+1)-(x-1)*( \frac{x-1}{4}+1)= = \frac{1}{2} (x-1)^2*ln(x-1)+(x-1)ln(x-1)- \frac{1}{4}(x-1)^2-(x-1) == \frac{1}{4}(x-1)*(2(x-1)*ln(x-1)+4ln(x-1)-x)|^3_2= =\frac{1}{4}(3-1)(2(3-1)*ln(3-1)+4ln(3-1)-3--(\frac{1}{4}(2-1)(2(2-1)*ln(2-1)+4ln(2-1)-2)== \frac{1}{2}(4ln2+4ln2-3)-( \frac{1}{4}(2ln1+4ln1-2)= = \frac{1}{2}(8*0,6913-3)-( \frac{1}{4}(2*0+4*0-2))= =2,7652-1,5+0,5=1,77

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years